MATEMATICA

INDICE MATEMATICA 1.01 - Le espressioni 1.02 - Proprietà delle potenze 1.03 - Frazioni con le proprietà delle potenze 1.04 - Le proporzioni 1.05 - Calcolo del termine incognito di una proporzione 1.06 - Proporzioni continue 1.07 - Serie di rapporti uguali 1.08 - Determinazione di due numeri di cui si conosce la somma e il rapporto 1.09 - Determinazione di due numeri di cui si conosce la differenza e il rapporto 1.10 - 2.01 - Le funzioni matematiche 2.02 - I limiti 2.03 - Le derivate TABELLE

1.01 - Le espressioni L’ordine delle operazioni Come prima cosa analizziamo come si risolvono le espressioni aritmetiche che non contengono parentesi. Nel caso in cui abbiamo una sola operazione, come nell’esempio precedente, è chiaro come trovare la soluzione dell’espressione, quando invece le operazioni coinvolte sono più di una, ci sono delle regole che dobbiamo seguire per risolvere l’espressione. Queste regole riguardano l’ordine in cui vanno eseguite le diverse operazioni, in ordine di priorità: - Potenze - Moltiplicazioni e divisioni - Addizioni e sottrazioni A parità di priorità si procede nell’ordine in cui sono scritte cioè da sinistra verso destra. Ad esempio nella espressione 4 + 2 x 5 – 3 non ci sono potenze allora passiamo alle moltiplicazioni, ce n’è solo una 2 x 5 e si svolge per prima; la nostra espressione diventa: 4 + 10 – 3 A questo punto abbiamo solo addizioni e sottrazioni, che hanno la stessa priorità e quindi si svolgono nell’ordine in cui sono state scritte, iniziando con 4 + 10 l’espressione diventa 14 – 3 Adesso svolgendo l’ultima operazione 14 - 3 otteniamo la soluzione dell’espressione: 11 Attenzione: Se non avessimo seguito le regole per l’ordine delle operazioni ma l’avessimo eseguite solamente nell’ordine in cui sono scritte avremmo ottenuto un risultato diverso ed errato. Le parentesi nell’espressione aritmetica Le parentesi che vengono usate nelle espressioni aritmetiche possono essere di diverso tipo. Esistono 3 tipi di parentesi: le parentesi tonde, le parentesi quadre e le parentesi graffe. Per prime si svolgono le operazioni racchiuse in parentesi tonde ( ... ) Poi si passa alle operazioni racchiuse tra parentesi quadre [ ... ] Per finire si passa alle operazioni racchiuse tra parentesi graffe { ... } Sempre seguendo le regole che gestiscono l’ordine delle operazioni! Finito di svolgere le operazioni all’interno di una parentesi, si elimina la parentesi. Esempio Consideriamo la seguente espressione con parentesi: [ 3 + (3 + 3 x 2 ) : 3 + ( 1 + 3 ) ] + 5 – 1 Si svolgono prima le operazioni tra parentesi tonde 3 + 3 x 2 e 1 + 3 rispettando l’ordine delle operazioni ( per svolgere 3 + 3 x 2 si calcola prima 3 x 2 e poi si calcola 3 + 6). La nostra espressione diventa: [ 3 + 9 : 3 + 4 ] + 5 – 1 C'è un’unica parentesi quadrata che racchiude 3 + 9 : 3 + 4. Seguendo l’ordine delle operazioni (prima la divisione e poi le somme nell’ordine in cui sono scritte) la nostra espressione si semplifica in 10 + 5 - 1 Svolgendo gli ultimi conti otteniamo come risultato 15 – 1 = 14 che è la soluzione della nostra espressione. Chiaramente le regole che abbiamo qui esaminato si estendono al caso in cui i numeri non siano interi. Ricapitolando: 1° TIPO - L'ESPRESSIONE NON CONTIENE PARENTESI: In questo caso bisogna risolvere l'espressione come segue: PRIMA SI RISOLVONO LE POTENZE; POI SI ESEGUONO MOLTIPLICAZIONI E DIVISIONI NELL'ORDINE IN CUI SI TROVANO; INFINE SI ESEGUONO LE ADDIZIONI E LE SOTTRAZIONI NELL'ORDINE IN CUI SI TROVANO; 2° TIPO - L'ESPRESSIONE CONTIENE PARENTESI: In questo caso bisogna risolvere l'espressione come segue: PRIMA SI ESEGUONO LE OPERAZIONI NELLE PARENTESI TONDE ( ), POI QUELLE NELLE PARENTESI QUADRE [ ] ED INFINE QUELLE NELLE PARENTESI GRAFFE { } secondo il seguente ordine: PRIMA LE POTENZE; POI LE MOLTIPLICAZIONI E LE DIVISIONI; INFINE SOMME E SOTTRAZIONI. Inoltre ricordiamo che una volta eseguite tutte le operazioni all'interno di una parentesi essa va eliminata. Vediamo un Esempio:

Notiamo che, a volte, le espressioni con frazioni si possono presentare nel modo seguente:

In questo caso ci troviamo di fronte ad una ESPRESSIONE con FRAZIONI a TERMINI FRAZIONARI. Questo tipo di espressioni aritmetiche frazionarie si risolvono considerando, come abbiamo visto nella lezione precedente

Quindi essa può essere risolta nel modo che segue:

Esempio:

1.02 - Proprietà delle potenze Nelle espressioni aritmetiche e nelle espressioni algebriche compaiono spesso operazioni con le potenze che, almeno inizialmente, possono sembrare difficili o laboriose: le proprietà delle potenze. Le proprietà delle potenze sono regole che permettono di risolvere in modo veloce e semplice le operazioni in cui compaiono le potenze. 1. Prodotto di potenze con la stessa base Il prodotto di due o più potenze che hanno la stessa base è una potenza che ha per base la stessa base e per esponente la somma degli esponenti. Vediamo alcuni Esempi: 4² * 4⁴ = 4⁽²⁺⁴⁾ = 4⁶ 7⁵ * 7³ = 7⁽⁵⁺³⁾ = 4⁸ 2. Quoziente di potenze con la stessa base La divisione tra due potenze che hanno la stessa base dà come risultato una potenza che ha per base la stessa base e per esponente la differenza degli esponenti. Vediamo alcuni Esempi: 6⁵ : 6³ = 6^(5-3) = 6² 2⁷ : 2⁴ = 2^(7-4) = 2³ 3. Potenza di potenza La potenza di una potenza è una potenza che ha per base la stessa base e per esponente il prodotto degli esponenti. Vediamo alcuni Esempi: (6²)⁴ = 6^2*4 = 6⁸ 4. Prodotto di potenze con lo stesso esponente Il prodotto di due o più potenze che hanno lo stesso esponente è una potenza che ha per base il prodotto delle basi e per esponente lo stesso esponente. Vediamo alcuni Esempi: 4² * 7² = (4 * 7)² = 28² 3⁴ * 5⁴ = (3 * 5)⁴ = 15⁴ 5. Quoziente di potenze con lo stesso esponente La divisione di due potenze che hanno lo stesso esponente dà come risultato una potenza che ha per base la divisione delle basi per esponente lo stesso esponente. Vediamo alcuni Esempi: 42⁵ : 6⁵ = (42 : 6)⁵ = 7⁵ 16⁴ : 4⁴ = (16 : 4)⁴ = 4⁴

1.03 - Frazioni con le proprietà delle potenze Come si applicano le proprietà delle potenze alle frazioni? - Per prima cosa si applicano le regole in base alla specifica proprietà delle potenze - In seguito si applicano gli esponenti alla frazione risultante, ottenendo il risultato finale Vediamo alcuni esempi, specifici per ogni proprietà.

1.04 - Le proporzioni Due rapporti si dicono uguali se hanno lo stesso valore, cioè: 15 : 5 = 3 e 21 : 7 = 3 Possiamo allora scrivere che 15 : 5 = 21 : 7 oppure 15/5 = 21/7 Un'uguaglianza di questo tipo si chiama proporzione, quindi una proporzione è un'uguaglianza tra due rapporti. Torniamo alla nostra proporzione: 15 : 5 = 21 : 7 essa si legge 15 sta a 5 come 21 sta a 7 I numeri indicati nella proporzione si chiamano termini della proporzione. In particolare il primo termine (nel nostro caso 15) e il quarto termine (nel nostro caso 7) si dicono estremi. Mentre il secondo termine (nel nostro caso 5) e il terzo termine (nel nostro caso 21) si dicono medi. Schematicamente:

Inoltre il primo e il terzo termine della proporzione si dicono antecedenti, mentre il secondo e il quarto termine si dicono conseguenti. Schematicamente:

Le 5 proprieta' delle proporzioni 1. Proprietà fondamentale Ci dice che, in ogni proporzione, il prodotto dei medi è uguale al prodotto degli estremi. Consideriamo la seguente proporzione: 15 : 5 = 21 : 7 Come abbiamo appreso nella lezione precedente, 5 e 21 sono i termini MEDI della proporzione e 15 e 7 sono i termini ESTREMI della proporzione. La nostra proporzione, Npuò essere scritta anche così 15/5 = 21/7 Ora riduciamo le due frazioni allo stesso denominatore, ovvero al prodotto dei due denominatori 5 e 7: 15 x 7/5 x 7 = 21 x 5/7 x 5 risolvendo: 15 x 7/35 = 21 x 5/35 Le nostre due frazioni sono uguali. Poiché le frazioni hanno il denominatore uguale, esse saranno uguali solamente se sono uguali anche i numeratori. Pertanto dovrà essere che: 15 x 7 = 21 x 5 Ora osserviamo questa uguaglianza e confrontiamola con la nostra proporzione di partenza: 15 : 5 = 21 : 7 15 x 7 non è altro che il prodotto degli estremi della proporzione. Mentre 21 x 5 non è altro che il prodotto dei medi della proporzione. Ecco, allora, che abbiamo dimostrato che in ogni proporzione, il prodotto dei medi è uguale al prodotto degli estremi. 2. Proprietà del permutare Consideriamo sempre la nostra proporzione: 15 : 5 = 21 : 7 e notiamo che, se in essa scambiamo i due medi, avremo: 15 : 21 = 5 : 7 ovvero avremo una nuova proporzione dato che il prodotto dei medi è sempre uguale al prodotto degli estremi. La stessa cosa succede se scambiamo tra loro i due estremi della proporzione. Infatti: 7 : 5 = 21 : 15 Anche in questo caso avremo una nuova proporzione dato che il prodotto dei medi è uguale al prodotto degli estremi. Questa proprietà delle proporzioni,cioè scambiare tra loro i due medi, o i due estremi, si chiama proprieta' del permutare 3. Proprietà dell'invertire Nella proporzione 15 : 5 = 21 : 7 e notiamo che, se in essa scambiamo ogni antecedente con il suo conseguente, avremo: 5 : 15 = 7 : 21 ovvero avremo una nuova proporzione dato che il prodotto dei medi è sempre uguale al prodotto degli estremi. Questa proprietà delle proporzioni,quella di scambiare ogni antecedente con il suo conseguente, si chiama proprieta' del permutare. 4. Proprietà del comporre Consideriamo sempre la nostra proporzione: 15 : 5 = 21 : 7 Ora sostituiamo al 1° termine la somma tra il 1° e il 2° termine, al 3° termine la somma tra il 3° e il 4° termine. Avremo: (15+5) : 5 = (21+7) : 7 Eseguendo le somme si avrà: 20 : 5 = 28 : 7 In questo caso notiamo il prodotto dei medi è uguale al prodotto degli estremi. In altre parole abbiamo visto che, in una proporzione, la somma del 1° e del 2° termine sta al 2° termine come la somma del 3° e del 4° termine sta al 4° termine. Notiamo però, che vale anche la seguente proprietà: la somma del 1° e del 2° termine sta al 1° termine come la somma del 3° e del 4° termine sta al 3° termine. Infatti: (15+5) : 15 = (21+7) : 21 risolvendo: 20 : 15 = 28 : 21 Questa proprietà delle proporzioni, quella che dice che il prodotto dei medi è uguale al prodotto degli estremi, si chiama proprieta' del comporre. 5. Proprietà dello scomporre Consideriamo sempre la nostra proporzione: 15 : 5 = 21 : 7 Se sostituiamo al 1° termine la differenza tra il 1° e il 2° termine e al al 3° termine la differenza tra il 3° e il 4° termine avremo: (15-5) : 5 = (-7) : 7 eseguendo le differenze si avrà 10 : 5 = 14 : 7 Questa proprietà delle proporzioni, quella che dice che il prodotto dei medi è uguale al prodotto degli estremi. In altre parole abbiamo visto che, in una proporzione, la differenza del 1° e del 2° termine sta al 2° termine come la differenza del terzo e del 4° termine sta al 4° termine. notiamo però, che vale anche la seguente proprietà: la differenza del 1° e del 2° termine sta al 1° termine come la differenza del 3° e del 4° termine sta al 3° termine. Infatti: (15-5) : 15 = (21-7) : 21 risolvendo: 10 : 15 = 14 : 21 eseguiamo il prodotto dei medi e verifichiamo che esso è uguale al prodotto degli estremi. la proprietà che abbiamo appena vista si dice proprieta' dello scomporre. Essa afferma che in una proporzione, la differenza del 1° e del 2° termine sta al 2° termine (o al 2° termine) come la differenza del 2° e del 4° termine sta al 3° termine (o al 4° termine). Vediamo alcuni Esempi: (8 - x) : x = 27 : 9 (8 - x + x) : x = (27 + 9) : 9 8 : x = 36 : 9 x = (8 x 9)/36 = 72/36 = 2 risolta applicando la proprietà dello comporre 3 : 2 = (x + 6) : x 1 : 2 = 6 : x x = (6 x 2)/1 = 12/1 = 12 risolta applicando la proprietà dello scomporre Come abbiamo avuto modo di vedere data una proporzione, applicando le proprieta' del permutare e dell'invertire e quelle del comporre e dello scomporre, se ne possono scrivere molte altre. Infatti:

1.05 - Calcolo del termine incognito di una proporzione Immaginiamo di conoscere tre termini di una proporzione e di voler calcolare il quarto termine. Esso verrà indicato con x e si chiamerà termine incognito. Esempio:: 18 : 3 = 24 : X Per trovare il termine incognito utilizziamo la proprietà fondamentale delle proporzioni che ci dice che il prodotto dei medi è uguale al prodotto degli estremi, quindi possiamo scrivere: 3 * 24 = 18 * X 72 = 18 * X 72 / 18 = X X = 4 quindi la proporzione è: 18 : 3 = 24 : 4 Quindi, ricapitolando: - se il termine incognito è un estremo esso si determina dividendo il prodotto dei medi per l'altro estremo; - se il termine incognito è un medio esso si determina dividendo il prodotto degli estremi per l'altro medio.

1.06 - Proporzioni continue Una proporzione con i due medi uguali si dice continua Esempio: 20 : 10 = 10 : 5 In una proporzione continua uno dei due medi uguali prende il nome di medio proporzionale fra i due estremi. Il quarto termine è detto terzo proporzionale dopo i primi due termini. Tornando alla proporzione continua che abbiamo scritto inizialmente avremo:

Come sappiamo la proprietà fondamentale delle proporzioni dice che, in ogni proporzione il prodotto dei medi è uguale al prodotto degli estremi. Ora, poiché nelle proporzioni continue i due medi sono uguali, questa proprietà potrà essere enunciata nel modo seguente: in ogni proporzione continua il prodotto degli estremi è uguale al quadrato dei medi. Infatti: 10 * 10 = 20 * 5 10² = 20 x 5 Ora vediamo come si risolve una proporzione continua. Consideriamo una proporzione continua nella quale il medio proporzionale sia il termine incognito. Ad esempio : 2 : X = X : 50 Essendo (per la proprietà fondamentale) che in ogni proporzione continua il prodotto degli estremi è uguale al quadrato dei medi, avremo: X² = 2 * 50 X² = 100 E' evidente che il valore di x lo otteniamo estraendo la radice quadrata di 100. Quindi: X = √10 X = 10 Quindi possiamo affermare che in una proporzione continua il medio incognito è uguale alla radice quadrata del prodotto degli estremi.

1.07 - Serie di rapporti uguali Consideriamo i seguenti rapporti: 15 : 3 = 5; 20 : 4 = 5; 30 : 6 = 5; 55 : 11 = 5 Notiamo che questi rapporti sono tutti uguali tra loro. Quindi possiamo scrivere: 15 : 3 = 20 : 4 = 30 : 6 = 55 : 11 Quella che abbiamo scritto è una serie di rapporti uguali o anche catena di rapporti uguali. Quindi una serie di rapporti uguali è l'uguaglianza di più di due rapporti. Data una serie di rapporti uguali, la somma degli antecedenti sta alla somma dei conseguenti, come un antecedente sta al suo conseguente. Scriviamo in ROSSO gli antecedenti e in BLU i conseguenti: 15 : 3 = 20 : 4 = 30 : 6 = 55 : 11 (15 + 20 + 30 + 55) : (3 + 4 + 6 + 11) = 15 : 3 (15 + 20 + 30 + 55) : (3 + 4 + 6 + 11) = 20 : 4 (15 + 20 + 30 + 55) : (3 + 4 + 6 + 11) = 30 : 6 (15 + 20 + 30 + 55) : (3 + 4 + 6 + 11) = 55 : 11 Ora prendiamo una di queste serie di rapporti uguali: (15 + 20 + 30 + 55) : (3 + 4 + 6 + 11) = 15 : 3 (15 + 20 + 30 + 55) : (3 + 4 + 6 + 11) = 15 : 3 120 : 24 = 15 : 3 Abbiamo così ottenuto una nuova proporzione. Infatti, il prodotto dei medi è uguali al prodotto degli estremi: 24 x 15 = 360 120 x 3 = 360 La proprietà che abbiamo appena visto prende il nome di proprietà del componendo degli antecedenti e dei conseguenti. Se in una catena di rapporti sono incogniti tutti gli antecedenti o tutti i conseguenti, ma si conosce la loro somma, si può applicare la proprietà precedente. Esempio: sappiamo che x : 5 = y : 2 = z : 4 e che x + y + z = 22 Ora possiamo risolvere le tre proporzioni come di consueto (x + y + z) : (5 + 2 + 4) = x : 5 22 : 11 = x : 5 x = (22 x 5)/ 11 = 110/11 = 10 (x + y + z) : (5 + 2 + 4) = y : 2 22 : 11 = y : 2 y = (22 x 2)/ 11 = 44/11 = 4 (x + y + z) : (5 + 2 + 4) = z : 4 22 : 11 = z : 4 z = (22 x 4)/ 11 = 88/11 = 8 Abbiamo così trovato i tre termini incogniti.

1.08 - Determinazione di due numeri di cui si conosce la somma e il rapporto La proprietà del comporre può risultare utile per risolvere alcuni problemi nei quali si conosce la somma di due numeri e il loro rapporto. Esempio: determinare due numeri sapendo che la loro somma è 35 e il loro rapporto è 4/3. Indichiamo con x e y i due numeri. Noi sappiamo che: x + y = 35 e che x : y = 4 : 3 La proprietà del comporre ci dice che in una proporzione, la somma del 1° e del 2° termine sta al 1° termine (o al 2° termine) come la somma del 3° e del 4° termine sta al 3° termine (o al 4° termine). Quindi noi possiamo scrivere: (x + y) : x = (4 + 3) : 4 (x + y) : y = (4 + 3) : 3 Ma noi sappiamo che x + y = 35 quindi possiamo scrivere: 35 : x = (4 + 3) : 4 35 : x = 7 : 4 35 : y = (4 + 3) : 3 35 : y = 7 : 3 Ora possiamo risolvere come sempre, ovvero: x = (35 x 4)/ 7 = 140/7 = 20 y = (35 x 3)/ 7 = 105/7 = 15 I due numeri cercati sono 20 e 15.

1.09 - Determinazione di due numeri di cui si conosce la differenza e il rapporto La proprietà dello scomporre può risultare utile per risolvere alcuni problemi nei quali si conosce la differenza di due numeri e il loro rapporto. Esempio: determinare due numeri sapendo che la loro differenza è 6 e il loro rapporto è 8/7. indichiamo con x e y i due numeri. Noi sappiamo che: x - y = 6 e che x : y = 8 : 7 La proprieta' dello scomporre ci dice che in una proporzione, la differenza del 1° e del 2° termine sta al 1° termine (o al 2° termine) come la differenza del 3° e del 4° termine sta al 3° termine (o al 4° termine). Quindi noi possiamo scrivere: (x - y) : x = (8 - 7) : 8 (x - y) : y = (8 - 7) : 7 Ma noi sappiamo che x - y = 6 quindi possiamo scrivere: 6 : x = (8 - 7) : 8 6 : x = 1 : 8 6 : y = (8 - 7) : 7 6 : y = 1 : 7 Ora possiamo risolvere come sempre, ovvero: x = (6 x 8)/ 1 = 48/1 =48 y = (6 x 7)/ 1 = 42/1 = 42 I due numeri cercati sono 48 e 42.

1.10 -

2.01 - Le funzioni matematiche Cosa sono le funzioni matematiche Dati due insiemi A e B, una funzione è una relazione che associa ad ogni numero reale di A uno e un solo numero di B. Per esempio se prendiamo in considerazione la funzione y=3x+5, questa associa a ogni valore di x un solo valore di y. L’insieme A viene detto dominio della funzione, mentre l’inseme B, formato dalle immagini degli elementi di A, è detto codominio. Allo stesso modo la x viene detta variabile indipendente e la y variabile dipendente perché appunto dipende dai valori attribuiti alla x. Esistono due forme per descrivere una funzione: la forma implicita (-3x+y-5=0) e la forma esplicita (y=3x+5) che è la più usata. Classificazione delle funzioni Una funzione algebrica può essere: - Razionale intera (o polinomiale) quando al suo interno contiene dei polinomi. Se sono di primo grado sarà lineare, se di secondo grado la chiameremo quadratica. - Razionale fratta se contiene al denominatore l’incognita x. - Irrazionale se la variabile x è contenuta all’interno di una radice. Esistono altri tipi di funzioni che non sono algebriche e si chiamano trascendenti, come ad esempio la funzione y=sin(x) o la funzione esponenziale y=e^x. Il dominio di una funzione Chiameremo dominio della funzione l’insieme più grande dei valori reali che si possono assegnare alla x affinché esista il corrispondente valore della y. Detto in questo modo, trovare il dominio di una funzione può sembrare una cosa molto complicata; in realtà è molto più facile a farsi che a dirsi. Per prima cosa ci conviene trovare il campo (o condizioni) di esistenza della funzione che molto spesso viene erroneamente confuso con lo stesso dominio. Il C.E. non è altro che l’insieme dei valori della x per i quali la funzione è definita. Se quindi, per esempio, abbiamo la funzione y=(3x+2)/(x-5), essa non esisterà nel caso in cui il denominatore sia uguale a 0; pertanto il nostro campo di esistenza sarà C.E.: x≠5. Per indicare il dominio, invece, scriveremo: D=]-8,5[U]5,+8[; dove le parentesi quadre indicano gli intervalli i cui valori possono essere assegnati alla funzione affinché esistano dei valori della y. Se due funzioni hanno lo stesso dominio, esse sono funzioni uguali. Proprietà delle funzioni Funzione iniettiva Prendendo in considerazione due insiemi A e B, una funzione viene definita iniettiva se ogni elemento di B è immagine al più di un elemento di A. Ciò significa che se per esempio prendiamo in considerazione una funzione qualsiasi del tipo y=ƒ(x), ogni valore delle y deve essere associato al massimo ad un solo valore delle ascisse (come la retta in figura). La funzione della parabola nella seconda figura, non può essere definita iniettiva perché per uno stesso valore delle ordinate corrispondono ben due valori delle x.

Funzione suriettiva Un altro tipo di funzioni sono quelle suriettive, ovvero in cui ogni elemento di B è immagine almeno di un elemento di A. Quindi qualunque valore tu scelga sull’asse delle y deve essere associato almeno ad un elemento delle x. Nell’immagine che segue è rappresentata una funzione suriettiva perché, come potrai vedere, a qualunque punto delle ordinate ne corrisponde almeno uno delle ascisse, anzi a volte ne corrispondono anche di più.

La seconda funzione, invece, esiste solo al di sopra dell’asse x, quindi nessuna ordinata negativa può essere associata con una x; pertanto la funzione non è suriettiva.

Funzione biunivoca Una funzione si dice biunivoca o biettiva se è sia iniettiva e sia suriettiva, quindi se ogni valore scelto sull’asse y corrisponde ad uno e un solo valore sull’asse x; come nel caso in figura.

Funzioni pari e dispari - Una funzione è pari quando ƒ(-x)=ƒ(x), essa quindi sarà simmetrica rispetto all’asse delle ordinate (come nella figura 1). Una funzione del tipo y=x²+1 è pari, perché, calcolando ƒ(-x), avremo che ƒ(-x)=(-x)²+1 ? y=x²+1, ovvero ƒ(x). - Se in una funzione ƒ(-x)=-ƒ(x), allora questa sarà dispari, e, come il grafico della seconda figura, sarà simmetrica rispetto all’origine degli assi. Ad esempio, y=x)³-x è una funzione dispari perché ƒ(-x)=(-x)³-(-x)=-x³+x che equivale a y=-(x³-x) quindi è vero che ƒ(-x)=-ƒ(x).

Le funzioni però non sono come i numeri che devono essere per forza pari o dispari. Una funzione infatti può anche non possedere nessuna delle due proprietà, in questo caso diremo che non c’è parità. Nel caso della funzione y=x³-1, se calcolassimo ƒ(-x), otterremmo una funzione diversa da quella di partenza, ovvero y=(-x)³-1=-x³-1=-(x³+1), che non coincide né con ƒ(x) e né con -ƒ(x). Pertanto la funzione non sarà simmetrica né con l’asse y e né con l’origine. Funzioni periodiche Considerando una funzione y=ƒ(x), viene definita periodica, di periodo T, se, per qualsiasi numero k intero, si ha: ƒ(x)=ƒ(x+kT). Essendo periodica, una funzione di questo tipo si ripete nel grafico in ogni intervallo T; le funzioni sin(x) e cos(x) ad esempio ripetono il loro andamento ogni 2π, mentre le funzioni tangente e cotangente hanno come periodo π.

Funzioni inverse Data la funzione biunivoca y = ƒ(x) da A a B, la funzione inversa di f è la funzione biunivoca x = ƒ^(-1)(y) da B ad A. Quando una funzione ammette la sua inversa, allora si dice invertibile. Nel caso in cui non lo fosse, è possibile effettuare una restrizione del dominio per rendere la funzione biunivoca. Ricorda!: il grafico di una funzione e quello della sua inversa sono simmetrici rispetto alla bisettrice del primo e del terzo quadrante.

2.02 - I limiti Il concetto di limite nacque in fisica per definire un intervallo di tempo molto piccolo. Per calcolare la velocità istantanea, infatti, bisogna considerare intervalli di tempo sempre più piccoli, arrivando quasi a far coincidere due punti (per esempio, A con B). In questo caso, Δ_t (l'intervallo di tempo) tende a 0 senza mai arrivare però a toccarlo, quindi:

“0” rappresenta il punto di accumulazione.

In matematica si utilizzano i limiti per studiare il comportamento delle funzioni. Per esempio nella funzione:

ci si può porre la domanda di come si comporti la funzione nell’intorno del valore 1. Che valore assuma la funzione vicino a 1? Con il limite si studia il comportamento della funzione non nel punto 1, ma vicino ad esso. Facciamo un altro esempio:

La funzione esiste solo per X ≠ 2 in quanto se x=2 si ha y=0/0. E' possibile però sostituire alla x valori poco più piccoli e poco più grandi di 2 e vedere come si comporta la funzione:

Notiamo che, avvicinandoci a X=2, il valore di y si avvicina a 4. Nell’avvicinarsi a 4, l’ intorno completo di 2 è sempre più piccolo (da 1 a 0,02). La differenza tra la funzione e il valore 4 è sempre minore, così che si può affermare che:

2.03 - Le derivate La derivata di una funzione f in un punto x₀ è il valore del coefficiente angolare della retta tangente alla curva nel punto, cioè la tangente trigonometrica dell'angolo formato dalla tangente in un punto della curva di equazione y=f(x)} e l'asse delle ascisse. Se la derivata è uguale a zero la retta tangente alla curva di equazione y=f(x) risulta parallela all'asse delle ascisse, mentre se la derivata tende a infinito la retta tangente alla curva di equazione y=f(x) è parallela all'asse delle ordinate. La funzione derivata si ricava con una serie di operazioni algebriche note come regole di derivazione, applicabili universalmente a tutte le funzioni derivabili.

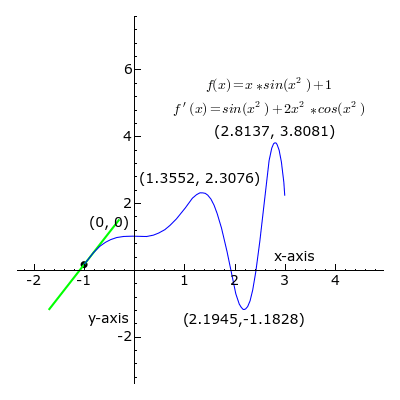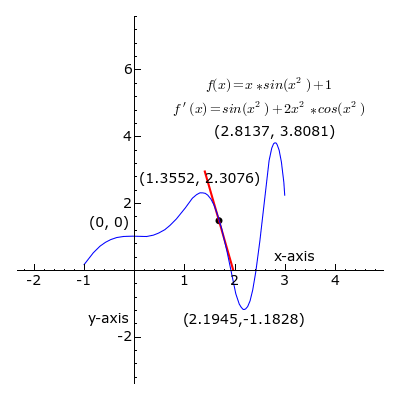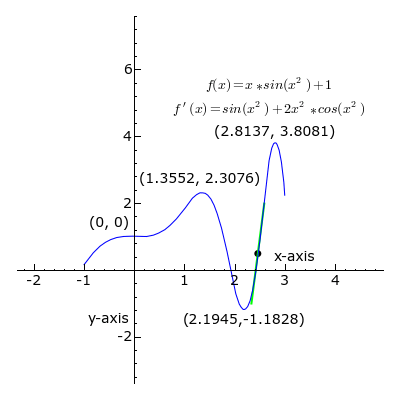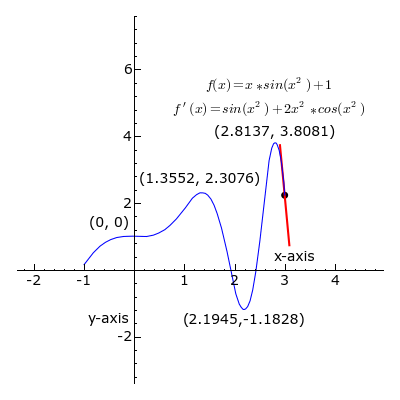Figura 1 La derivata di una funzione in un punto è il coefficiente angolare della retta tangente alla curva nel punto. Si tratta quindi di un numero che misura la pendenza della retta tangente. Definizione analitica di derivata In analisi matematica la derivata di una funzione reale di variabile reale f(x) nel punto x₀ è definita come il limite del rapporto incrementale al tendere a 0 dell’incremento h, sotto l’ipotesi che tale limite esista e sia finito. Più precisamente, una data funzione f(x) definita in un intorno di x₀ si dice derivabile nel punto x₀ se esiste ed è finito il limite:

ed il valore di questo limite prende il nome di derivata della funzione nel punto x₀. Se la funzione f(x) è derivabile in ogni punto di un dato intervallo (a, b), allora si dice che essa è derivabile in (a, b), e la funzione f^I(x) che associa ad ogni punto x la derivata di f in x è la funzione derivata di f. Si chiama derivata destra di f in x₀ il:

Si chiama derivata sinistra di f in x₀ il:

Esempi dal sito matematicaoltre:

2.04 -

2.05 -

TABELLE Vediamo un esempio chiarificatore: Nella tabella sotto basta considerare la 1° e la 3° colonna; sulla 3° cerchi il simbolo e ti segni il valore ad es. cm (simbolo = c) e valore = 10^-2 poi cerchi il simbolo di quello che devi convertire, ad es. Kilo (simbolo = k) e valore 10³ dopo di che conti quanta distanza c'è tra -2 e +3, quindi 5 Quindi per passare da cm a Km dovrai moltiplicare per 10^-5 poichè si SALE nella tabella. Per il contrario invece, da Km a cm, dovrai moltiplicare per 10⁵ perchè si SCENDE nella tabella. Nel caso sopra se sono Km² moltiplichi l'esponete x2 se Km³ x3 cioè: Da cm² a Km² dovrai moltiplicare per 10^-10 mentre per passare da Km² a cm², dovrai moltiplicare per 10¹⁰ Da cm³ a Km³ dovrai moltiplicare per 10^-15 mentre per passare da Km³ a cm³, dovrai moltiplicare per 10¹⁵

Multipli e sottomultipli 1

Volume in litri, con fattore di conversione tra dm³ e i litri