2. LE MISURE DELLE GRANDEZZE FISICHE
3. I VETTORI E LE FORZE
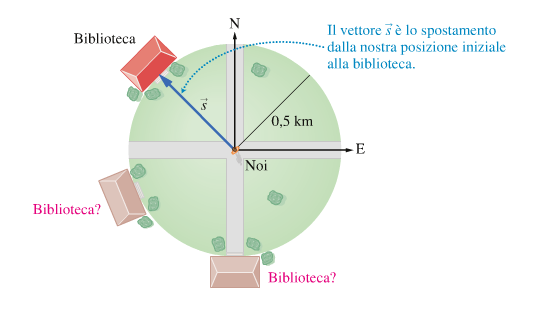 Lo spostamento da punto dove siamo alla biblioteca è una grandezza fisica determinata dalla distanza e dalla direzione.
Nella figura sopra lo spostamento è rappresentato da una freccia che punta nella direzione e nel verso del moto e
la cui lunghezza che chiameremo modulo o intensità (500m nel nostro caso) rappresenta la distanza in linea d'aria tra noi e la biblioteca.
Questo spostamento è un ESEMPIO di grandezza vettoriale.
PS: una grandezza scalare è una grandezza che viene descritta unicamente, dal punto di vista matematico, da un numero reale, detto anch'esso scalare,
spesso associato a un'unità di misura. A differenza delle grandezze vettoriali, non è pertanto sensibile alle dimensioni dello spazio, né al particolare
sistema di riferimento o di coordinate utilizzato.
Definiamo grandezza vettoriale una grandezza fisica rappresentata graficamente da un vettore.
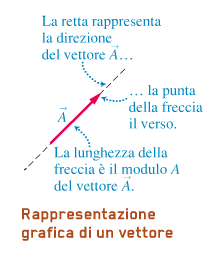
Un vettore è un ente matematico definito da un modulo (che è un numero NON negativo), una direzione e un verso.
Alcuni ESEMPI di grandezze vettoriali sono: lo spostamento, la velocità e l'accelerazione di un oggetto e le forze.
La rappresentazione grafica di un vettore è la seguente:
Lo spostamento da punto dove siamo alla biblioteca è una grandezza fisica determinata dalla distanza e dalla direzione.
Nella figura sopra lo spostamento è rappresentato da una freccia che punta nella direzione e nel verso del moto e
la cui lunghezza che chiameremo modulo o intensità (500m nel nostro caso) rappresenta la distanza in linea d'aria tra noi e la biblioteca.
Questo spostamento è un ESEMPIO di grandezza vettoriale.
PS: una grandezza scalare è una grandezza che viene descritta unicamente, dal punto di vista matematico, da un numero reale, detto anch'esso scalare,
spesso associato a un'unità di misura. A differenza delle grandezze vettoriali, non è pertanto sensibile alle dimensioni dello spazio, né al particolare
sistema di riferimento o di coordinate utilizzato.
Definiamo grandezza vettoriale una grandezza fisica rappresentata graficamente da un vettore.
Un vettore è un ente matematico definito da un modulo (che è un numero NON negativo), una direzione e un verso.
Alcuni ESEMPI di grandezze vettoriali sono: lo spostamento, la velocità e l'accelerazione di un oggetto e le forze.
La rappresentazione grafica di un vettore è la seguente:
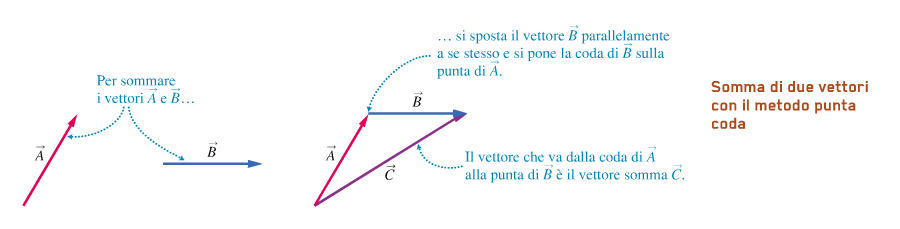
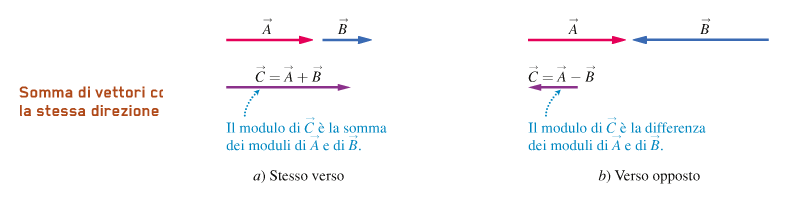
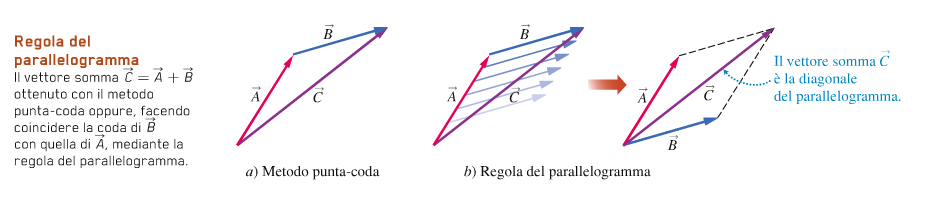
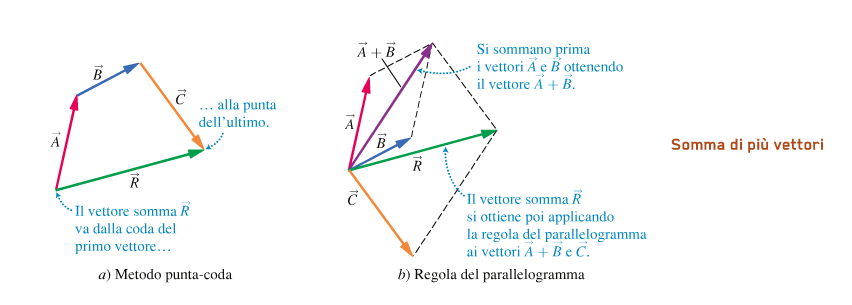
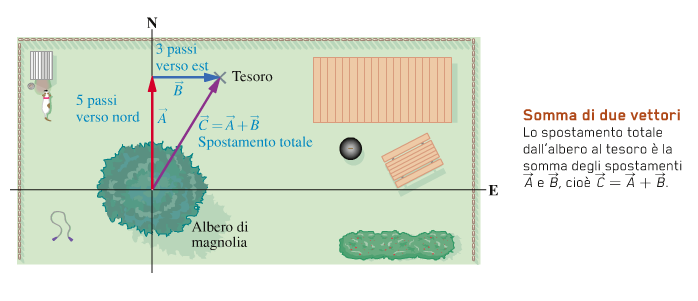 La regola che si segue per la somma e detto metodo punta-coda: per sommare due vettori A e B:
1) si dispone la coda di B sulla punta di A
2) la somma C = A + B è il vettore che va dalla coda A alla punta di B.
Per farlo è necessario spostare i vettori, operazione possibile se spostati parallelamente a se stessi, senza modificare la lunghezza e il verso.
La regola che si segue per la somma e detto metodo punta-coda: per sommare due vettori A e B:
1) si dispone la coda di B sulla punta di A
2) la somma C = A + B è il vettore che va dalla coda A alla punta di B.
Per farlo è necessario spostare i vettori, operazione possibile se spostati parallelamente a se stessi, senza modificare la lunghezza e il verso.

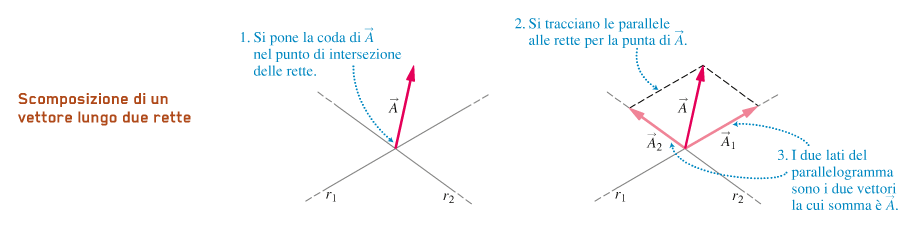
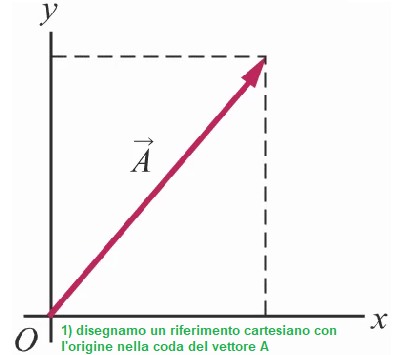
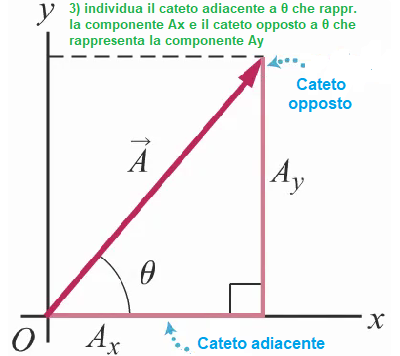
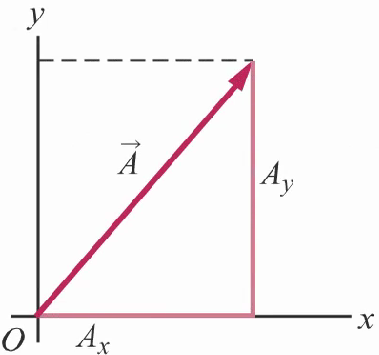
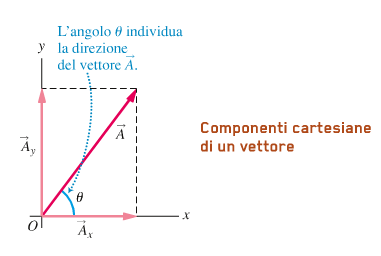 Ponendo la coda di un vettore A nell'origine O e disegnando le parallele degli assi x e y che passano per la punta di A, si trovano due vettori perpendicolari
Ax e Ay la cui somma è A:
A= Ax + Ay
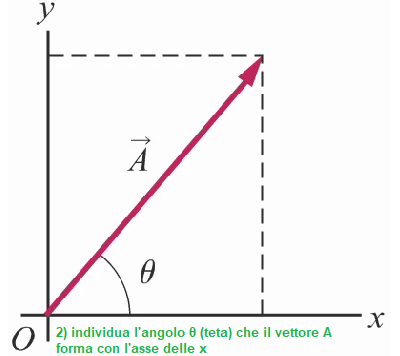
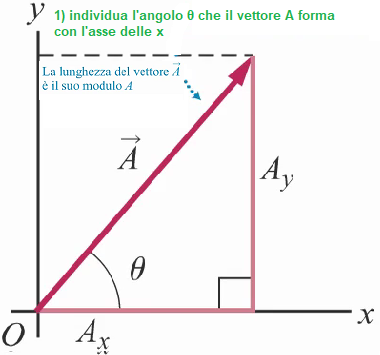
La direzione di A nel sistema cartesiano è individuata dall'angolo θ che il vettore forma con l'asse delle ascisse x.
I moduli Ax e Ay dei due vettori Ax e Ay sono le componenti cartesiane del vettore A.
Ad esse è attribuito un segno positivo o negativo a seconda che i vettori Ax e Ay siano diretti nel verso positivo o negativo degli assi x e y.
Graficamente:
Ponendo la coda di un vettore A nell'origine O e disegnando le parallele degli assi x e y che passano per la punta di A, si trovano due vettori perpendicolari
Ax e Ay la cui somma è A:
A= Ax + Ay
La direzione di A nel sistema cartesiano è individuata dall'angolo θ che il vettore forma con l'asse delle ascisse x.
I moduli Ax e Ay dei due vettori Ax e Ay sono le componenti cartesiane del vettore A.
Ad esse è attribuito un segno positivo o negativo a seconda che i vettori Ax e Ay siano diretti nel verso positivo o negativo degli assi x e y.
Graficamente:
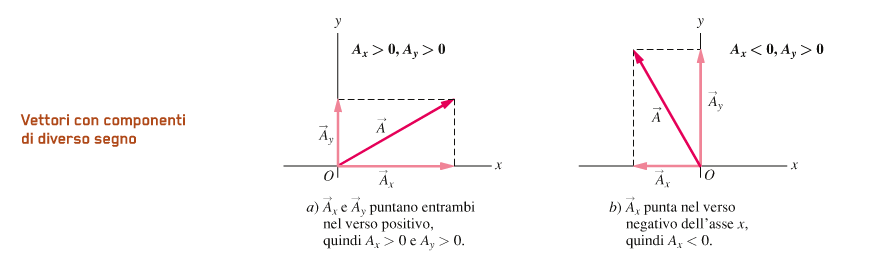
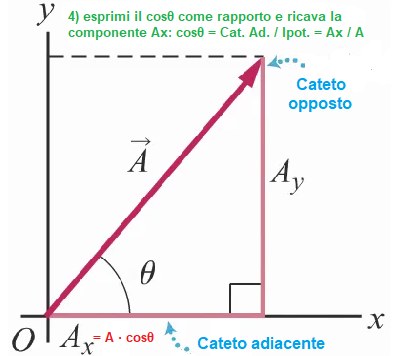
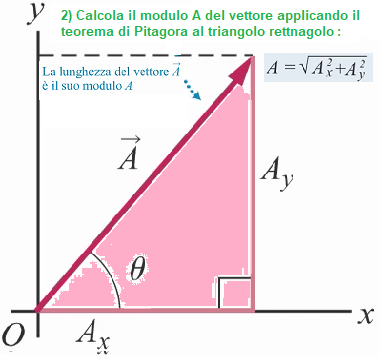
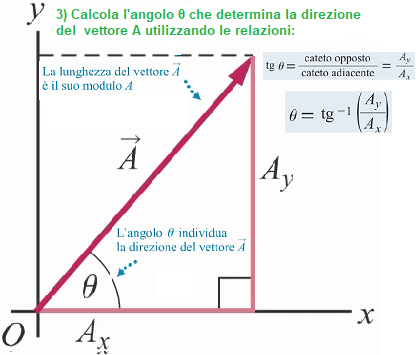
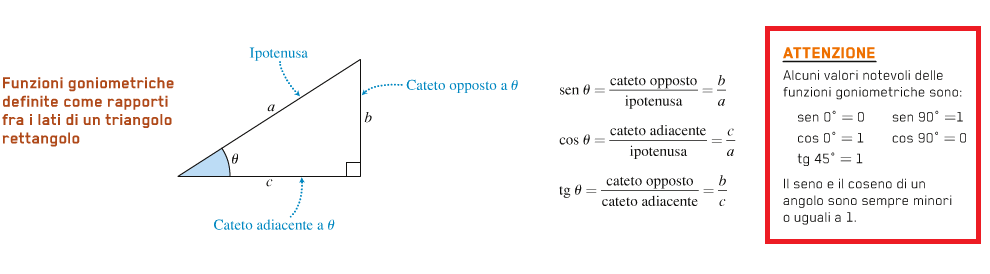 Dalla figura sopra possiamo scrivere le seguenti relazioni che rappresentano il seno coseno e tangente di un angolo θ
sen θ = b / a → b = a * sen θ
cos θ = c / a → c = a * cos θ
tg θ = b / c → b = c * tg θ → c = b / tg θ
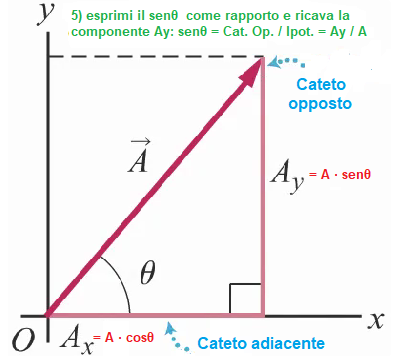
Dalla figura sopra possiamo scrivere le seguenti relazioni che rappresentano il seno coseno e tangente di un angolo θ
sen θ = b / a → b = a * sen θ
cos θ = c / a → c = a * cos θ
tg θ = b / c → b = c * tg θ → c = b / tg θ
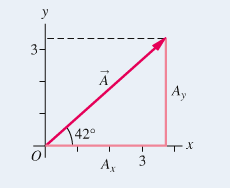 Ricaviamo ora la componente Ax = A * cos θ = 5cm * cos 42° = 5cm * 0,74 = 3,72 cm
Ricaviamo ora la componente Ay = A * sen θ = 5cm * sen 42° = 5cm * 0,67 = 3,35 cm
Ricaviamo ora la componente Ax = A * cos θ = 5cm * cos 42° = 5cm * 0,74 = 3,72 cm
Ricaviamo ora la componente Ay = A * sen θ = 5cm * sen 42° = 5cm * 0,67 = 3,35 cm
Le relazioni usate nei 2 esercizi sopra si possono utilizzare anche per calcolare il problema inverso cioè calcolare il modulo di un vettore e l'angolo che identifica la sua direzione, conoscnedo le componenti cartesiane del vettore.
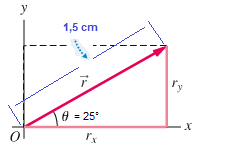 Le componenti cartesiane rx e ry del vettore r si ottengono applicando relazioni:
rx = r * cos θ = 1,5m * cos 25° = 1,5m * 0,9063 = 1,36m
ry = r * sen θ = 1,5m * sen 25° = 1,5m * 0,4226 = 0,634m
Per verifica risolviamo il problema inverso: date le componenti rx = 1,36m ed ry = 0,634m calcoliamo il modulo e la direzione di r:
r = √ (rx)2 + (ry)2 = √ (1,36m)2 + (0,634m)2 = √ 1,85m2 + 0.4m2 = 2,25m2 = 1,5m
tg θ = rx / ry = 0,634 / 1,36 = 0,4662 → θ = tg-1 * 0,4662 = tasti calcolatrice: [2nd] [tan] e digito: 0,4662 = 25°
Le componenti cartesiane rx e ry del vettore r si ottengono applicando relazioni:
rx = r * cos θ = 1,5m * cos 25° = 1,5m * 0,9063 = 1,36m
ry = r * sen θ = 1,5m * sen 25° = 1,5m * 0,4226 = 0,634m
Per verifica risolviamo il problema inverso: date le componenti rx = 1,36m ed ry = 0,634m calcoliamo il modulo e la direzione di r:
r = √ (rx)2 + (ry)2 = √ (1,36m)2 + (0,634m)2 = √ 1,85m2 + 0.4m2 = 2,25m2 = 1,5m
tg θ = rx / ry = 0,634 / 1,36 = 0,4662 → θ = tg-1 * 0,4662 = tasti calcolatrice: [2nd] [tan] e digito: 0,4662 = 25°
ESEMPI di calcolo funzioni trigonomertriche su calcolatrice scientifica:

Facciamo ora un paio di esempi che capirne lutilità.
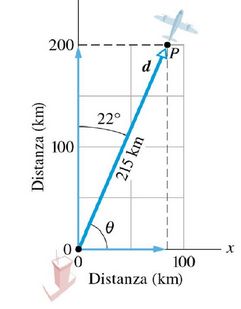 Proviamo ora a fare i calcoli:
dx = d * cos θ = (215 km) * (cos 68°) = 81 km
dy = d * sen θ = (215 km) * (sen 68°) = 109 km
Proviamo ora a fare i calcoli:
dx = d * cos θ = (215 km) * (cos 68°) = 81 km
dy = d * sen θ = (215 km) * (sen 68°) = 109 km
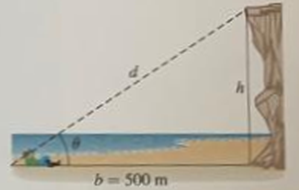 DESCRIZIONE DEL PROBLEMA In figura è disegnato il triangolo rettangolo che rappresenta il modello del problema. Il lato opposto all'angolo θ è l'altezza h
della scogliera che dobbiamo determinare, mentre il lato adiacente all'angolo è la distazna b = 500m; a questo punto si sdraia per terra e misura l'angolo fra
la linea orizzontale e la direzione in cui vede la cima della scogliera e l'uomo.
STRATEGIA Usiamo la funzione coseno e la relazione tra cateti, ipotenusa e angoli di un triangolo rettangolo.
SOLUZIONE Dalla relazione b = d * cos θ calcoliamo d:
d = b / cos θ = 500m / cos 34° = 603m
Usando il teorema di Pitagora possiamo ora scrivere l'altezza h:
h =√ d2 - b2 = √ (603m)2 - (500m)2 = √ 363.609m2 - 250.000m2 = √ 113.609m2 = 337,06m
OSSERVAZIONI Per calcolare l'altezza h è fondamentale conoscere la distanza b del punto di osservazione della base della scogliera, quindi la scogliera deve
essere accessibile.
DESCRIZIONE DEL PROBLEMA In figura è disegnato il triangolo rettangolo che rappresenta il modello del problema. Il lato opposto all'angolo θ è l'altezza h
della scogliera che dobbiamo determinare, mentre il lato adiacente all'angolo è la distazna b = 500m; a questo punto si sdraia per terra e misura l'angolo fra
la linea orizzontale e la direzione in cui vede la cima della scogliera e l'uomo.
STRATEGIA Usiamo la funzione coseno e la relazione tra cateti, ipotenusa e angoli di un triangolo rettangolo.
SOLUZIONE Dalla relazione b = d * cos θ calcoliamo d:
d = b / cos θ = 500m / cos 34° = 603m
Usando il teorema di Pitagora possiamo ora scrivere l'altezza h:
h =√ d2 - b2 = √ (603m)2 - (500m)2 = √ 363.609m2 - 250.000m2 = √ 113.609m2 = 337,06m
OSSERVAZIONI Per calcolare l'altezza h è fondamentale conoscere la distanza b del punto di osservazione della base della scogliera, quindi la scogliera deve
essere accessibile.
PROBLEMA 3: se √ fosse di 30°, a quale distanza si troverebbe l'uomo dalla base della scogliera? d = 603 (dato ricavato dall'PROBLEMA 2) b = 603 * cos 30° = 603 * 0,866 = 522,21
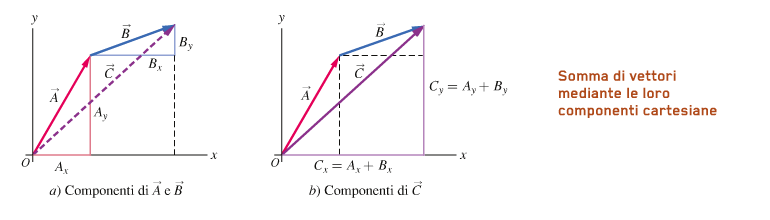
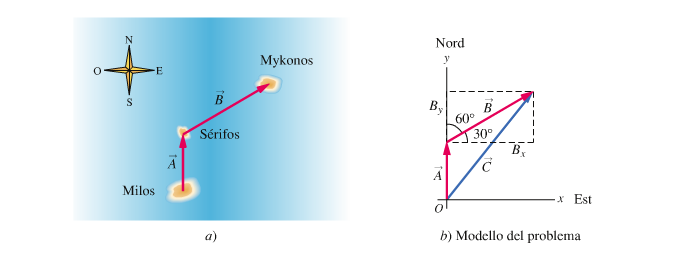 DESCRIZIONE DEL PROBLEMA In figura a) sono tracciati i vettori spostamento da Milos a Serifos (A) e da Serifos a Mykonos (B).
I moduli di questi vettori sono 24 nmi e 42 nmi, rispettivamente. Continueremo a usare le miglia nautiche come unità di misura della lunghezza.
Dobbiamo determina il modulo dello spostamento totale C = A + B da Milos a Mykonos.
STRATEGIA Cotruiamo il modello del problema, in figura b).
Poniamo l'origine O di un sistema di assi cartesiani nel punto di partenza (Milos). Gli assi sono orientati in modo che le ascisse (x) puntino a est e le
ordinate (y) a nord. Calcoliamo le componenti cartesiane di A e B, osservando che A è diretto lungo l'asse y e B forma con l'asse orinzontale un angolo di 30°.
Le componenti Cx e Cy di C sono la somma delle componenti Ax e Ay di A e Bx e By di B.
A partire da Cx e Cy determiniamo C usando il teorema di Pitagora.
SOLUZIONE Le componenti di A sono:
Ax = 0 nmi
Ay = 24 nmi
Le componenti di B sono:
Bx = 42 nmi * cos 30° = 42 nmi * 0,86 = 36 nmi
By = 24 nmi * sen 30° = 24 nmi * 0,5 = 21 nmi
Le componenti di C si ottengono sommando quelle di A e quelle di B :
Cx = Ax + Bx = 0 nmi + 36 nmi = 36 nmi
Cy = Ay + By = 24 nmi + 21 nmi = 45 nmi
Il modulo di C è dato da
C = √ (Cx)2 + (Cy)2 = √ (36 nmi)2 + (45 nmi>)2 = √ 1296 + 2025 = √ 3321 = 58 nmi
SOLUZIONE Il modulo dello spostamento NON è uguale alla distanza percorsa dalla barca, che è 24+42= 66 nmi
DESCRIZIONE DEL PROBLEMA In figura a) sono tracciati i vettori spostamento da Milos a Serifos (A) e da Serifos a Mykonos (B).
I moduli di questi vettori sono 24 nmi e 42 nmi, rispettivamente. Continueremo a usare le miglia nautiche come unità di misura della lunghezza.
Dobbiamo determina il modulo dello spostamento totale C = A + B da Milos a Mykonos.
STRATEGIA Cotruiamo il modello del problema, in figura b).
Poniamo l'origine O di un sistema di assi cartesiani nel punto di partenza (Milos). Gli assi sono orientati in modo che le ascisse (x) puntino a est e le
ordinate (y) a nord. Calcoliamo le componenti cartesiane di A e B, osservando che A è diretto lungo l'asse y e B forma con l'asse orinzontale un angolo di 30°.
Le componenti Cx e Cy di C sono la somma delle componenti Ax e Ay di A e Bx e By di B.
A partire da Cx e Cy determiniamo C usando il teorema di Pitagora.
SOLUZIONE Le componenti di A sono:
Ax = 0 nmi
Ay = 24 nmi
Le componenti di B sono:
Bx = 42 nmi * cos 30° = 42 nmi * 0,86 = 36 nmi
By = 24 nmi * sen 30° = 24 nmi * 0,5 = 21 nmi
Le componenti di C si ottengono sommando quelle di A e quelle di B :
Cx = Ax + Bx = 0 nmi + 36 nmi = 36 nmi
Cy = Ay + By = 24 nmi + 21 nmi = 45 nmi
Il modulo di C è dato da
C = √ (Cx)2 + (Cy)2 = √ (36 nmi)2 + (45 nmi>)2 = √ 1296 + 2025 = √ 3321 = 58 nmi
SOLUZIONE Il modulo dello spostamento NON è uguale alla distanza percorsa dalla barca, che è 24+42= 66 nmi
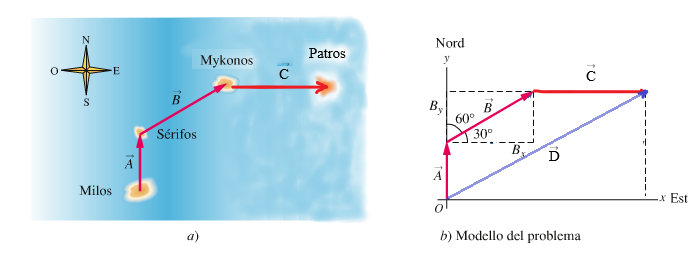 SOLUZIONE Le componenti di A sono:
Ax = 0 nmi
Ay = 24 nmi
Le componenti di B sono:
Bx = 42 nmi * cos 30° = 42 nmi * 0,86 = 36 nmi
By = 24 nmi * sen 30° = 24 nmi * 0,5 = 21 nmi
Le componenti di C sono:
Cx = 80 nmi
Cy = 0 nmi
Le componenti di D si ottengono sommando quelle di A, B e C:
Dx = Ax + Bx + Cx = 0 nmi + 36 nmi + 80 nmi = 116 nmi
Dy = Ay + By + Cy = 24 nmi + 21 nmi + 0 nmi = 45 nmi
Il modulo di C è dato da
C = √ (Cx)2 + (Cy)2 = √ (116 nmi)2 + (45 nmi>)2 = √ 13465 + 2025 = √ 15481 = 124 nmi
SOLUZIONE Le componenti di A sono:
Ax = 0 nmi
Ay = 24 nmi
Le componenti di B sono:
Bx = 42 nmi * cos 30° = 42 nmi * 0,86 = 36 nmi
By = 24 nmi * sen 30° = 24 nmi * 0,5 = 21 nmi
Le componenti di C sono:
Cx = 80 nmi
Cy = 0 nmi
Le componenti di D si ottengono sommando quelle di A, B e C:
Dx = Ax + Bx + Cx = 0 nmi + 36 nmi + 80 nmi = 116 nmi
Dy = Ay + By + Cy = 24 nmi + 21 nmi + 0 nmi = 45 nmi
Il modulo di C è dato da
C = √ (Cx)2 + (Cy)2 = √ (116 nmi)2 + (45 nmi>)2 = √ 13465 + 2025 = √ 15481 = 124 nmi

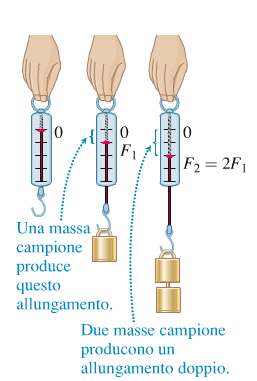 Possiamo definire l'unità di misura della forza, che è il newton (N), come la forza che produce un allungamento della molla di un dinamometro
uguale a quello prodotto da una massa appesa di (1 / 9,81 = 0,1019) kg.
Vediamo alcuni esempi di intensità di forze:
Possiamo definire l'unità di misura della forza, che è il newton (N), come la forza che produce un allungamento della molla di un dinamometro
uguale a quello prodotto da una massa appesa di (1 / 9,81 = 0,1019) kg.
Vediamo alcuni esempi di intensità di forze:
| Tipi di forza | Intensità (N) |
| Forza dei motori di una navicella | 3,1 * 107 |
| Forza trainante di una locomotiva | 2,5 * 105 |
| Spinta del motore di un jet | 7,5 * 104 |
| Forza per accelerare un'auto | 7 * 103 |
| Peso di un uono adulto | 7 * 102 |
| Peso di una mela | 1 |
| Peso di una rosa | 1 * 10-1 |
| Peso di una formica | 1 * 10-3 |
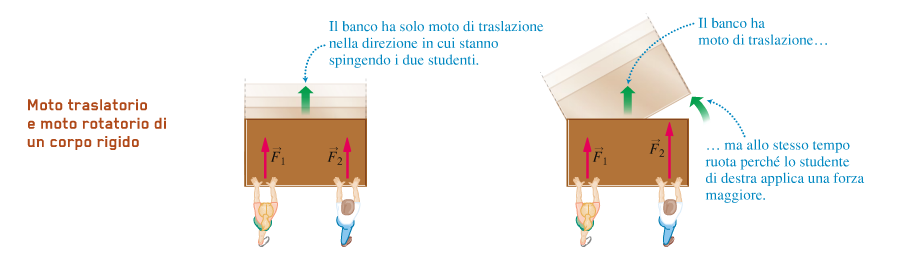
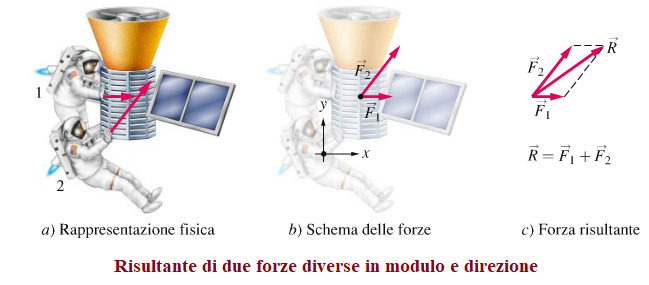
ESEMPIO 1: supponiamo che due astronauti usino i propulsori a getto per spingere un satellite verso la navicella spaziale come in figura sotto. Se l'astronauta 1 esercita una forza F1 e l'astronauta 2 esercita una forza F2, la risultante delle forze sul satellite, cioè la forza effettiva che agisce sul satellite, è la somma vettoriale: R = F1 + F2
 Poichè le forze si sommano vettorialmente, è possibile che su un corpo agiscano delle forze singolarmente non nulle, ma la cui risultante è nulla.
In questo caso si duce che il corpo è in equilibrio
Poichè le forze si sommano vettorialmente, è possibile che su un corpo agiscano delle forze singolarmente non nulle, ma la cui risultante è nulla.
In questo caso si duce che il corpo è in equilibrio
ESEMPIO 2: se gli astronauti dell'esempio 1 spingono il satellite con forze di intensità F1=26 N ed F2=41 N, le cui direzioni formano un angolo di 52°, qual'è l'intensità della forza risultante sul satellite? DESCRIZIONE DEL PROBLEMA Con il sistema di coordinate indicato nel'esempio 1 l'astronauta 1 spinge nel verso positivo dell'asse x, mentre l'astronauta 2 spinge con un angolo di 52° rispetto allo stesso asse. L'astronaita 1 esercita una forza di intensità F1=26 N, l'astronauta 2 esercita una forza di intensità F2=41 N. Dobbiamo quindi calcolare il modulo di R = F1 + F2.
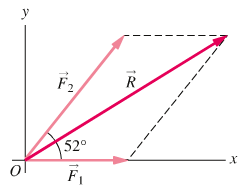 STRATEGIA Usiamo il metodo della somma vettoriale per componenti cartesiane. Calcoliamo le componenti cartesiane di F1 e F2, le sommiamo per ricavare
quelle di R, che permettono di determinare il modulo R.
SOLUZIONE F1 è diretto lungo l'asse x, quindi le sue componenti sono:
F1x = F1 = 26 N
F1y = 0
F2 forma un angolo di 52° con l'asse x. Le sue componenti sono:
F2x = F2 * cos 52° = (41 N) cos 52° = 41 N * 0,6157 = 25,24 N
F2y = F2 * sen 52° = (41 N) sen 52° = 41 N * 0,7880 = 32,31 N
Le componenti di R sono la somma delle componenti di F1 e di F2:
Rx = F1x + F2x = (26+25,24) N = 51,24 N
Ry = F1y + F2y = (0+32,31) N = 32,31 N
Il modulo di R si ottiene con la formula (approssimo i valori trovati sopra all'unità):
R = √ (Rx)2 + (Ry)2 = √ (51 N)2 + (32 N)2 = √ 2.601 N2 + 1.024 N2 = √ 3.625? N2 = 60 N
STRATEGIA Usiamo il metodo della somma vettoriale per componenti cartesiane. Calcoliamo le componenti cartesiane di F1 e F2, le sommiamo per ricavare
quelle di R, che permettono di determinare il modulo R.
SOLUZIONE F1 è diretto lungo l'asse x, quindi le sue componenti sono:
F1x = F1 = 26 N
F1y = 0
F2 forma un angolo di 52° con l'asse x. Le sue componenti sono:
F2x = F2 * cos 52° = (41 N) cos 52° = 41 N * 0,6157 = 25,24 N
F2y = F2 * sen 52° = (41 N) sen 52° = 41 N * 0,7880 = 32,31 N
Le componenti di R sono la somma delle componenti di F1 e di F2:
Rx = F1x + F2x = (26+25,24) N = 51,24 N
Ry = F1y + F2y = (0+32,31) N = 32,31 N
Il modulo di R si ottiene con la formula (approssimo i valori trovati sopra all'unità):
R = √ (Rx)2 + (Ry)2 = √ (51 N)2 + (32 N)2 = √ 2.601 N2 + 1.024 N2 = √ 3.625? N2 = 60 N
ESEMPIO 3: Quanto varrebbe il modulo di R se le forze F1 ed F2 fossero perpendicolari DESCRIZIONE DEL PROBLEMA E' lo stesso problema dell'esempio 2 ma l'angolo fra le forze è di 90°.
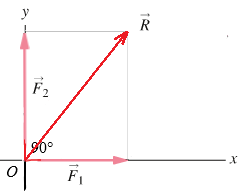 SOLUZIONE F1 è diretto lungo l'asse x, quindi le sue componenti sono:
F1x = F1 = 26 N
F1y = 0
F2 è diretto lungo l'asse y. Le sue componenti sono:
F2x = 0
F2y = F2 = 41 N
Le componenti di R sono la somma delle componenti di F1 e di F2:
Rx = F1x + F2x = (26+0) N = 26 N
Ry = F1y + F2y = (0+41) N = 41 N
Il modulo di R si ottiene con la formula (approssimo i valori trovati sopra all'unità):
R = √ (Rx)2 + (Ry)2 = √ (26 N)2 + (41 N)2 = √ 676 N2 + 1.681 N2 = √2.357 N2 = 48,55 N
SOLUZIONE F1 è diretto lungo l'asse x, quindi le sue componenti sono:
F1x = F1 = 26 N
F1y = 0
F2 è diretto lungo l'asse y. Le sue componenti sono:
F2x = 0
F2y = F2 = 41 N
Le componenti di R sono la somma delle componenti di F1 e di F2:
Rx = F1x + F2x = (26+0) N = 26 N
Ry = F1y + F2y = (0+41) N = 41 N
Il modulo di R si ottiene con la formula (approssimo i valori trovati sopra all'unità):
R = √ (Rx)2 + (Ry)2 = √ (26 N)2 + (41 N)2 = √ 676 N2 + 1.681 N2 = √2.357 N2 = 48,55 N

ESEMPIO 1: la sonda Phoenix Mars Lander è atterrata su Marte il 25/5/2008 dopo 9 mesi di viaggio; ha massa m = 350 Kg. Qual'è il suo peso sulla Terra e su Marte (dove g = 3,69 N/Kg)? DESCRIZIONE DEL PROBLEMA La massa della sonda, che è la stessa su entrambi i pianeti, è m = 350 Kg. Dobbiamo calcolare il peso, che dipende della costante g, che vale 9,81 N/Kg sulla Terra e 3,69 N/Kg su Marte. STRATEGIA Usiamo al relazione tra massa e peso P = mg SOLUZIONE Il peso della sonda sulla Terra è: PTerra = m*gTerra = 350 Kg * 9,81 N/Kg = 3,43 * 103 N Il peso della sonda sulla Luna è: PLuna = m*gLuna = 350 Kg * 3,69 N/Kg = 1,29 * 103 N Proviamo a vedere il valore della sonda Phoenix Mars Lander sugl'altri pianeti del sistema solare (la Terra è il 3° e Marte il 4°):
| Il peso della sonda sulla Mercurio è: | PMercurio = m*gMercurio = 350 Kg * 3,7 N/Kg | = 1,295 * 103 N |
| Il peso della sonda sulla Venere è: | PVenere = m*gVenere = 350 Kg * 8,87 N/Kg | = 3,105 * 103 N |
| Il peso della sonda sulla Giove è: | PGiove = m*gGiove = 350 Kg * 23,12 N/Kg | = 8,092 * 103 N |
| Il peso della sonda sulla Saturno è: | PSaturno = m*gSaturno = 350 Kg * 8,96 N/Kg | = 3,136 * 103 N |
| Il peso della sonda sulla Urano è: | PUrano = m*gUrano = 350 Kg * 8,69 N/Kg | = 3,042 * 103 N |
| Il peso della sonda sulla Nettuno è: | PNettuno = m*gNettuno = 350 Kg * 11 N/Kg | = 3,85 * 103 N |
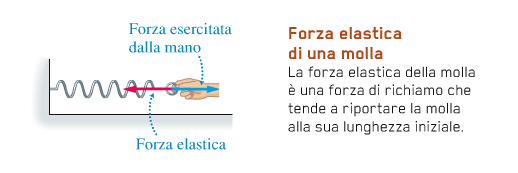
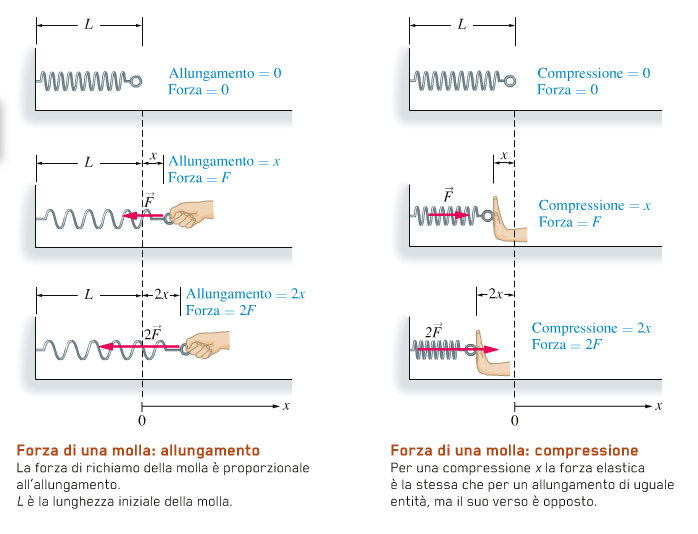 La forza elastica è quindi direttamente proporzionale all'allungamento.
Analogamente, se comprimiamo la molla di una quantità x, la molla spinge la mano con una forza elastica di intensità F, dove F ha
lo stesso valore del caso precedente. La compressione di 2x comporterà una spinta di 2F.
La differenza rispetto all'allungamento e che il verso della forza è opposto.
Definiamo la Legge di Hooke:
Una molla esercita una forza elastica la cui intensità F è direttamente proporzionale all'allungamento o alla compressione x della molla, in formule:
F = k * x
In queste espressione k è la costante di proporzionalità e prende il nome di costante elastica della molla.
Essendo F misurata in newton e x in metri l'unità di misura di k è il newton al metro N/m e più grande è il valore di k più rigida è la molla, cioè
maggiore è la forza alla quale dobbiamo sottoporre la molla per ottenere lo stesso allungamento.
Un ESEMPIO di utilizzo della Legge di Hooke è nei legami molecolari che possono essere rappresentati come "molle interatomiche":
La forza elastica è quindi direttamente proporzionale all'allungamento.
Analogamente, se comprimiamo la molla di una quantità x, la molla spinge la mano con una forza elastica di intensità F, dove F ha
lo stesso valore del caso precedente. La compressione di 2x comporterà una spinta di 2F.
La differenza rispetto all'allungamento e che il verso della forza è opposto.
Definiamo la Legge di Hooke:
Una molla esercita una forza elastica la cui intensità F è direttamente proporzionale all'allungamento o alla compressione x della molla, in formule:
F = k * x
In queste espressione k è la costante di proporzionalità e prende il nome di costante elastica della molla.
Essendo F misurata in newton e x in metri l'unità di misura di k è il newton al metro N/m e più grande è il valore di k più rigida è la molla, cioè
maggiore è la forza alla quale dobbiamo sottoporre la molla per ottenere lo stesso allungamento.
Un ESEMPIO di utilizzo della Legge di Hooke è nei legami molecolari che possono essere rappresentati come "molle interatomiche":
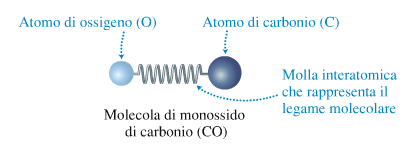 La legge di Hooke è una legge empiriche (cioè che non varia nel tempo e nello spazio) ma ovviamente non può valere per ogni valore di x.
Allungando troppo una molla questa si deforma permanentemente.
Si parla di molle ideali per indicare molle prive di massa che obbediscono esattamente alla legge di Hooke.
D'ora in poi per "molle" intenderemo sempre molle ideali.
Possiamo definire la Legge di Hooke in forma vettoriale:
Una molla che subisce uno spostamento x dalla posizione di equilibrio esercita una forza elastica data da:
F = -k * x
La legge di Hooke è una legge empiriche (cioè che non varia nel tempo e nello spazio) ma ovviamente non può valere per ogni valore di x.
Allungando troppo una molla questa si deforma permanentemente.
Si parla di molle ideali per indicare molle prive di massa che obbediscono esattamente alla legge di Hooke.
D'ora in poi per "molle" intenderemo sempre molle ideali.
Possiamo definire la Legge di Hooke in forma vettoriale:
Una molla che subisce uno spostamento x dalla posizione di equilibrio esercita una forza elastica data da:
F = -k * x
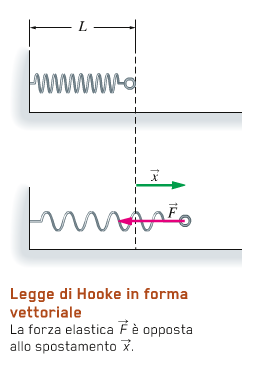 il segno meno ci dice che la forza elastica è sempre opposta allo spostamento della molla dalla posizione di equilibrio.
il segno meno ci dice che la forza elastica è sempre opposta allo spostamento della molla dalla posizione di equilibrio.
ESERCIZIO 1: Due molle 1 e 2 hanno rispettivamente costante elastiva k1=200 N/m e k2=100 N/m. a) se si applica a entrambe le molle la stessa forza di F = 4 N, quel'è il loro allungamento? b) rappresenta graficamente la legge di Hooke per le due molle. a) dalla legge di Hooke, F = k * x si ottiene che l'allungamento della molla 1 è: x = F / k1 = 4 N / 200 N/m = 0,02 m mentre l'allungamento della molla 2 è: x = F / k2 = 4 N / 100 N/m = 0,04 m cioè il doppio. b) la legge di Hooke per le due molle è rappresentata graficamente delle rette in figura.
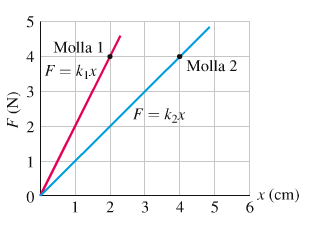 Notiamo che quanto più grande è la costante elastica, tanto più è ripida la retta che descrive la legge.
Notiamo che quanto più grande è la costante elastica, tanto più è ripida la retta che descrive la legge.
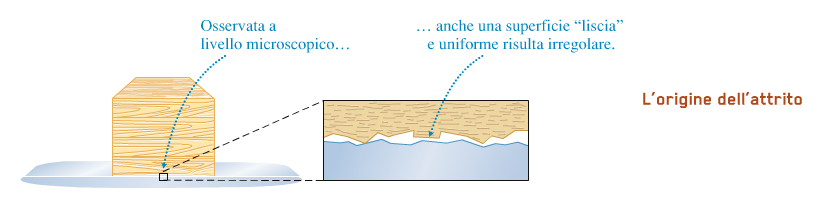 Poichè l'attrito dipende da molti fattori, ad ESEMPIO il materiale, la finitura della superficie, la presenza di lubrificanti, NON ESISTE una legge fisica
semplice e universale che lo descriva.
Ci sono però alcune leggi empiriche (da osservazioni si ricavano descrizioni di oggetti e altri fenomeni che NON variano a distanza di tempo e di spazio)
che permettono di calcolare le forze di attrito.
Una prima distinzione è quella fra l'attrito che si manifesta quando un corpo scivola su una superficie, detto attrito radente,
e l'attrito che si manifesta quando un corpo rotola su una superficie, detto attrito volvente.
L'attrito volvente volvente è molto meno intenso dell'attrito radente tra le stesse superfici.
C'è un ulteriore forma di attrito, detta attrito del mezzo o attrito viscoso, che si oppone al moto di un corpo in un mezzo fluido
(cioè in un gas o in un liquido) e che dipende dalla velocità del corpo.
La forza di attrito radente si distingue in :
- attrito dinamico, che si oppone allo scorrimento di un corpo su una superficie.
- attrito statico, che si oppone al distacco di un corpo da una superficie.
Come vedremo, la forza di attrito radente è proporzionale alla forza premente sulla superficie, ma è indipendente dalla superficie di contatto fra le superfici
ed è espressa dalla relazione:
= µ * F⊥
dove F⊥ è la forza premente sulla superficie, coiè la componente perpemndicolare della forza che agisce sulla superficie, e µ (mu) è il coefficiente di attrito.
Poichè l'attrito dipende da molti fattori, ad ESEMPIO il materiale, la finitura della superficie, la presenza di lubrificanti, NON ESISTE una legge fisica
semplice e universale che lo descriva.
Ci sono però alcune leggi empiriche (da osservazioni si ricavano descrizioni di oggetti e altri fenomeni che NON variano a distanza di tempo e di spazio)
che permettono di calcolare le forze di attrito.
Una prima distinzione è quella fra l'attrito che si manifesta quando un corpo scivola su una superficie, detto attrito radente,
e l'attrito che si manifesta quando un corpo rotola su una superficie, detto attrito volvente.
L'attrito volvente volvente è molto meno intenso dell'attrito radente tra le stesse superfici.
C'è un ulteriore forma di attrito, detta attrito del mezzo o attrito viscoso, che si oppone al moto di un corpo in un mezzo fluido
(cioè in un gas o in un liquido) e che dipende dalla velocità del corpo.
La forza di attrito radente si distingue in :
- attrito dinamico, che si oppone allo scorrimento di un corpo su una superficie.
- attrito statico, che si oppone al distacco di un corpo da una superficie.
Come vedremo, la forza di attrito radente è proporzionale alla forza premente sulla superficie, ma è indipendente dalla superficie di contatto fra le superfici
ed è espressa dalla relazione:
= µ * F⊥
dove F⊥ è la forza premente sulla superficie, coiè la componente perpemndicolare della forza che agisce sulla superficie, e µ (mu) è il coefficiente di attrito.
 Poichè Fattrito e F⊥ sono entrambe forze e hanno la stessa unità di misura µ è un numero adimensionale.
I suoi valori variano fra 0 e 1 e alcuni di essi sono riportati nella tabella sotto:
Poichè Fattrito e F⊥ sono entrambe forze e hanno la stessa unità di misura µ è un numero adimensionale.
I suoi valori variano fra 0 e 1 e alcuni di essi sono riportati nella tabella sotto:
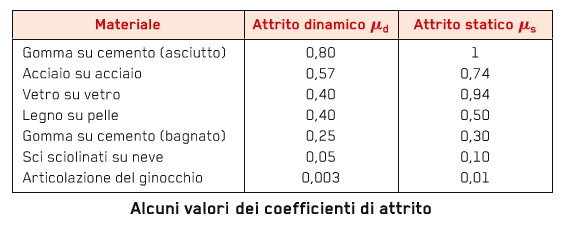 Come si nota in genere il coefficiente di attrito statico µs è maggiore del coefficiente di attrito dinamico µd e questo significa che la forza di attrito statico è
maggiore della forza di attrito dinamico.
La forza di attrito è una grandezza vettoriale, che ha direzione parallela alla superficie di contatto e ha verso opposto a quello dello scorrimento, nel caso di
attrito dinamico e a quello in cui si muoverebbe l'oggetto se non ci fosse attrito, nel caso di attrito statico.
Come si nota in genere il coefficiente di attrito statico µs è maggiore del coefficiente di attrito dinamico µd e questo significa che la forza di attrito statico è
maggiore della forza di attrito dinamico.
La forza di attrito è una grandezza vettoriale, che ha direzione parallela alla superficie di contatto e ha verso opposto a quello dello scorrimento, nel caso di
attrito dinamico e a quello in cui si muoverebbe l'oggetto se non ci fosse attrito, nel caso di attrito statico.
 Si può verificare sperimentalmente che la forza di attrito dinamico non dipende ne dall'area della superficie di contatto ne dalla velocità del corpo,
ma solo dalla forza che agisce perpendicolarmente alla superficie. In formule la legge dell'attrito dinamico è:
Fd = µd * F⊥
dove F⊥ è la forza premente perpendicolare e la costante di proporzionalità µd è il coefficiente di attrito dinamico.
Se il corpo che scivola sulla superficie non è soggetto ad alcuna forza esterna, la forza premente F⊥ è semplicemente data dal suo peso P.
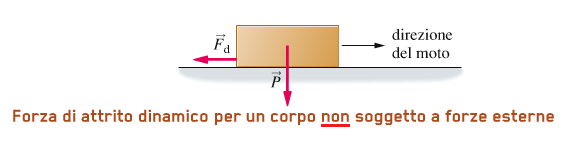
Consideriamo ad ESEMPIO 1 un mattone che scorre su una superficie orizzontale, non soggetto ad alcuna forza esterna:
In questo caso la forza di attrito dinamico agisce in direzione opposta al moto e dipende dal peso P del mattone:
Fd = µd * F⊥ = µd * P
Si può verificare sperimentalmente che la forza di attrito dinamico non dipende ne dall'area della superficie di contatto ne dalla velocità del corpo,
ma solo dalla forza che agisce perpendicolarmente alla superficie. In formule la legge dell'attrito dinamico è:
Fd = µd * F⊥
dove F⊥ è la forza premente perpendicolare e la costante di proporzionalità µd è il coefficiente di attrito dinamico.
Se il corpo che scivola sulla superficie non è soggetto ad alcuna forza esterna, la forza premente F⊥ è semplicemente data dal suo peso P.
Consideriamo ad ESEMPIO 1 un mattone che scorre su una superficie orizzontale, non soggetto ad alcuna forza esterna:
In questo caso la forza di attrito dinamico agisce in direzione opposta al moto e dipende dal peso P del mattone:
Fd = µd * F⊥ = µd * P
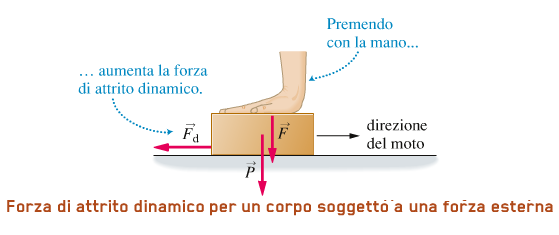
 ESEMPIO 2 Supponiamo ora di premere con la mano sul mattone con una forza F, in questo caso sulla superficie agisco due forze, F e P e quindi F⊥ = F + P.
L'attrito dinamico in questo caso è:
Fd = µd * F⊥ = µd * (P + F)
ESEMPIO 2 Supponiamo ora di premere con la mano sul mattone con una forza F, in questo caso sulla superficie agisco due forze, F e P e quindi F⊥ = F + P.
L'attrito dinamico in questo caso è:
Fd = µd * F⊥ = µd * (P + F)
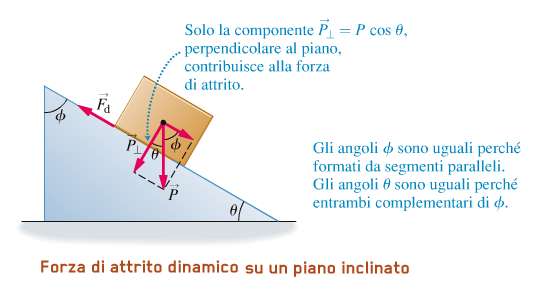
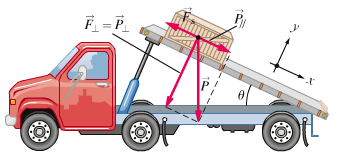
 ESEMPIO 3 Consideriamo ora lo scivolamento di un corpo lungo un piano inclinato. In questo caso la forza premente è la componente della forza peso
perpendicolare al piano, che è inferiore al modulo P della forza peso. E' solo questa componente che contribuisce alla froza di attrito.
Dalla figura sotto si vede che θ (theta) è l'angolo di inclinazione del piano, la forza premente è F⊥ = P⊥ = P cos θ ed è sempre minore del peso P.
La forza di attrito su un piano inclinato è quindi minore che su un piano orizzontale:
Fd = µd * F⊥ = µd * P * cos θ
ESEMPIO 3 Consideriamo ora lo scivolamento di un corpo lungo un piano inclinato. In questo caso la forza premente è la componente della forza peso
perpendicolare al piano, che è inferiore al modulo P della forza peso. E' solo questa componente che contribuisce alla froza di attrito.
Dalla figura sotto si vede che θ (theta) è l'angolo di inclinazione del piano, la forza premente è F⊥ = P⊥ = P cos θ ed è sempre minore del peso P.
La forza di attrito su un piano inclinato è quindi minore che su un piano orizzontale:
Fd = µd * F⊥ = µd * P * cos θ
 Riassumento:
Leggi empiriche dell'attrito dinamico
la forza di attrito dinamico tra un corpo e una superficie:
1) è parallela alla superficie di contatto e il suo verso è opposto a quello dello scivolamento del corpo sulla superficie;
2) è indipendente dall'area della superficie di contatto e dalla velocità vdel corpo;
3) è proporzionale alla forza premente sulla superficie, Fd = µd * F⊥
Riassumento:
Leggi empiriche dell'attrito dinamico
la forza di attrito dinamico tra un corpo e una superficie:
1) è parallela alla superficie di contatto e il suo verso è opposto a quello dello scivolamento del corpo sulla superficie;
2) è indipendente dall'area della superficie di contatto e dalla velocità vdel corpo;
3) è proporzionale alla forza premente sulla superficie, Fd = µd * F⊥
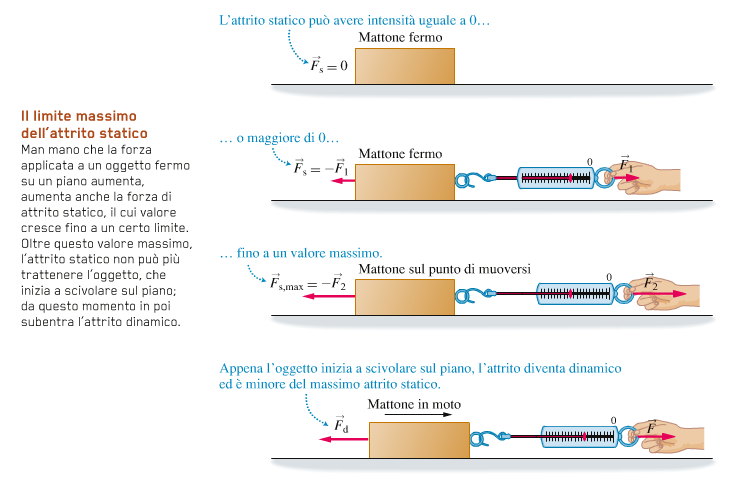 Se tiriamo il mattone con una forza così piccola da non riuscire a farlo muovere, sul mattone agisce una forza di attrito statico Fd che tende a mantenerlo
fermo, essendo uguale ed opposta alla forza che applichiamo sul mattone.
Aumentiamo ora gradualmente l'intensità della forza applicata.
Fino a che il mattone rimane fermo, aumenta anche la forza di attristo statico, che continua a compensare quella applicata.
A un certo punto il mattone comincia a muoversi e in quel momento la forza di attrito statico raggiunge il suo valore massimo che indicheremo con Fs,max.
Successivamente l'attrito diventa dinamico.
La Fs,max è detta forza massima di attrito statico o forza di attrito al distacco.
Si trova sperimentalmente che la forza massima di attrito statico NON dipende dall'area della superficie di contatto ed è direttamente proporzionale alla
forza premente:
Forza massima di attrito statico>
Fs,max = µs * F⊥
La costante di proporzionalità µs è il coefficiente di attrito statico.
FISICA REALE: il coefficiente di attrito statico dipende da molti fattori, incluso il fatto che le superfici siano asciutte o bagnate.
Nel deserto della Valle della morte, in California, le rare ma forti piogge rendono viscito il terreno sobbioso e possono a volte ridurre l'attrito tra le roccie e
il terreno in modo che i venti forti possono spostarle anche lontano.
Le osservazioni precedenti possono essere riassunte nelle seguenti leggi empiriche dell'attrito statico:
Leggi empiriche dell'attrito statico
la forza di attrito statico tra un corpo e una superficie:
1) è parallela alla superficie di contatto e il suo verso è opposto a quello in cui si muoverebbe il corpo in assenza di attrito;
2) è indipendente dall'area della superficie di contatto;
3) può assumere un qualsiasi valore tra zero e la forza massima di attrito statico Fs,max = µs * F⊥
Se tiriamo il mattone con una forza così piccola da non riuscire a farlo muovere, sul mattone agisce una forza di attrito statico Fd che tende a mantenerlo
fermo, essendo uguale ed opposta alla forza che applichiamo sul mattone.
Aumentiamo ora gradualmente l'intensità della forza applicata.
Fino a che il mattone rimane fermo, aumenta anche la forza di attristo statico, che continua a compensare quella applicata.
A un certo punto il mattone comincia a muoversi e in quel momento la forza di attrito statico raggiunge il suo valore massimo che indicheremo con Fs,max.
Successivamente l'attrito diventa dinamico.
La Fs,max è detta forza massima di attrito statico o forza di attrito al distacco.
Si trova sperimentalmente che la forza massima di attrito statico NON dipende dall'area della superficie di contatto ed è direttamente proporzionale alla
forza premente:
Forza massima di attrito statico>
Fs,max = µs * F⊥
La costante di proporzionalità µs è il coefficiente di attrito statico.
FISICA REALE: il coefficiente di attrito statico dipende da molti fattori, incluso il fatto che le superfici siano asciutte o bagnate.
Nel deserto della Valle della morte, in California, le rare ma forti piogge rendono viscito il terreno sobbioso e possono a volte ridurre l'attrito tra le roccie e
il terreno in modo che i venti forti possono spostarle anche lontano.
Le osservazioni precedenti possono essere riassunte nelle seguenti leggi empiriche dell'attrito statico:
Leggi empiriche dell'attrito statico
la forza di attrito statico tra un corpo e una superficie:
1) è parallela alla superficie di contatto e il suo verso è opposto a quello in cui si muoverebbe il corpo in assenza di attrito;
2) è indipendente dall'area della superficie di contatto;
3) può assumere un qualsiasi valore tra zero e la forza massima di attrito statico Fs,max = µs * F⊥
 STRATEGIA
a) Usiamo la condizione di equilibrio Fs = P// per determinare Fs.
b) Usiamo la relazione Fs,max = µs * F⊥ per determinare µs
SOLUZIONE
a) Calcoliamo la componente della forza peso parallela al pianale:
P// = mg * sen θ = 95 Kg * 9,81 N/Kg * sen 20° = 931,95 N * 0,34 = 319
Poichè la cassa è ferma, Fs = P// e quindi Fs = 319 N
b) Calcoliamo la componente della forza peso parallela al pianale, quando questo è inclinato di 32°:
P// = mg * sen θ = 95 Kg * 9,81 N/Kg * sen 32° = 931,95 N * 0,53 = 494 N
Poichè la cassa comincia a muoversi, la forza massima di attrito statico è Fs,max = 494 N
Calcoliamo la componente della forza peso perpendicolare al pianale:
F⊥ = P⊥ = mg * cos θ = 95 Kg * 9,81 N/Kg * cos 32° = 931,95 N * 0,85 = 790 N
Dalla relazione Fs,max = µs * F⊥ ricaviamo µs
µs = Fs,max / F⊥ = 494 N / 790 N = 0,695
STRATEGIA
a) Usiamo la condizione di equilibrio Fs = P// per determinare Fs.
b) Usiamo la relazione Fs,max = µs * F⊥ per determinare µs
SOLUZIONE
a) Calcoliamo la componente della forza peso parallela al pianale:
P// = mg * sen θ = 95 Kg * 9,81 N/Kg * sen 20° = 931,95 N * 0,34 = 319
Poichè la cassa è ferma, Fs = P// e quindi Fs = 319 N
b) Calcoliamo la componente della forza peso parallela al pianale, quando questo è inclinato di 32°:
P// = mg * sen θ = 95 Kg * 9,81 N/Kg * sen 32° = 931,95 N * 0,53 = 494 N
Poichè la cassa comincia a muoversi, la forza massima di attrito statico è Fs,max = 494 N
Calcoliamo la componente della forza peso perpendicolare al pianale:
F⊥ = P⊥ = mg * cos θ = 95 Kg * 9,81 N/Kg * cos 32° = 931,95 N * 0,85 = 790 N
Dalla relazione Fs,max = µs * F⊥ ricaviamo µs
µs = Fs,max / F⊥ = 494 N / 790 N = 0,695


4. L'EQUILIBRIO DEI SOLIDI L'equilibrio dei corpi è oggetto di quella parte della fisica classica chiamata statica. Studieremo le condizioni di equilibrio dei corpi solidi; inizieremo considerendo i punti materiali, per poi estendere il discorso ai corpi rigidi.
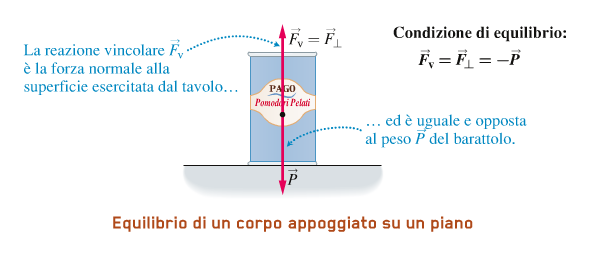 Imponiamo la condizione di equilibrio: in questo caso le forze sono dirette verso l'alto e una verso il basso, in direzione perpendicolare al tavolo.
La risultante R è data dalla somma vettoriale della forza peso e della reazione vincolare:
R = P + Fv
Poichè R = 0, abbiamo:
P + Fv cioè: Fv = – P
Consideriamo ora il caso in cui sul barattolo agisce una forza F diretta verso il basso, ad ESEMPIO quella esercitata dalla nostra mano.
Imponiamo la condizione di equilibrio: in questo caso le forze sono dirette verso l'alto e una verso il basso, in direzione perpendicolare al tavolo.
La risultante R è data dalla somma vettoriale della forza peso e della reazione vincolare:
R = P + Fv
Poichè R = 0, abbiamo:
P + Fv cioè: Fv = – P
Consideriamo ora il caso in cui sul barattolo agisce una forza F diretta verso il basso, ad ESEMPIO quella esercitata dalla nostra mano.
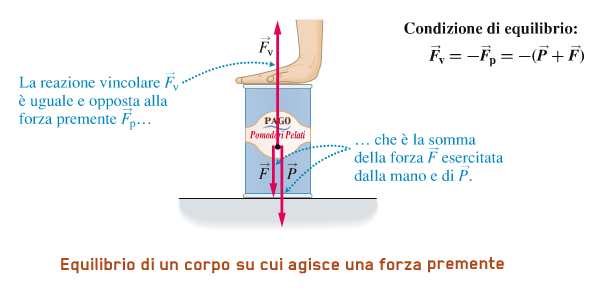 La risultante in questo caso è:
R = P + F + Fv
da cui, imponendo la condizione R = 0, si ottiene:
P + F + Fv = 0 cioè: Fv = – (P + F)
La reazione vincolare come si vede è maggiore del peso del parattolo ed è uguale e opposta a P + F, che è la forza premente Fp sulla superficie:
Fv = – Fp
In generale quindi:
Reazione vincolare Fv
La reazione vincolare Fv esercitata da una superficie è uguale e opposta alla forza premente Fp che agisce sulla superfice:
Fv = – Fp
Se le forze che agiscono su un punto materiale hanno direzioni diverse, la condizione di equilibrio rihiede che entrambe le componenti cartesiane della risultante R siano nulle, cioè:
Rx = 0
Ry = 0
Ad ESEMPIO, consideriamo il caso in cui sul barattolo agiscono due forze, una orizzontale F1, esercitata da una mano che spinge verso destra, e una inclinata di 30° rispetto alla
superficie del tavolo, F2, esercitata da una mano che spnge in direzione inclinata verso il basso.
La risultante in questo caso è:
R = P + F + Fv
da cui, imponendo la condizione R = 0, si ottiene:
P + F + Fv = 0 cioè: Fv = – (P + F)
La reazione vincolare come si vede è maggiore del peso del parattolo ed è uguale e opposta a P + F, che è la forza premente Fp sulla superficie:
Fv = – Fp
In generale quindi:
Reazione vincolare Fv
La reazione vincolare Fv esercitata da una superficie è uguale e opposta alla forza premente Fp che agisce sulla superfice:
Fv = – Fp
Se le forze che agiscono su un punto materiale hanno direzioni diverse, la condizione di equilibrio rihiede che entrambe le componenti cartesiane della risultante R siano nulle, cioè:
Rx = 0
Ry = 0
Ad ESEMPIO, consideriamo il caso in cui sul barattolo agiscono due forze, una orizzontale F1, esercitata da una mano che spinge verso destra, e una inclinata di 30° rispetto alla
superficie del tavolo, F2, esercitata da una mano che spnge in direzione inclinata verso il basso.
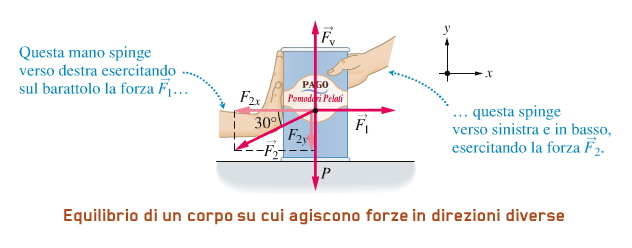 Scegliamo il sistema di assi come in figura sopra e scriviamo le componenti delle forze nelle direzioni x e y:
F1x = F1
F1y = 0
F2x = – F2 cos 30°
F2y = – F2 sen 30°
Le componenti della risultante R delle forze sono:
Rx = F1x + F2x
Ry = F1y + F2y + P + Fv
Se il barattolo è fermo le componenti Rx e Ry devono essere entrambe NULLE, quindi la condizione di equilibrio è:
Rx = 0 → F1x = – F2x
Ry = 0 → Fv = – (P + F1y + F2y)
Tenendo conto delle espressioni delle componenti delle forze, la condizione in questo cosa specifico si può scrivere:
F1 = – F2x
Fv = – (P + F2y)
Scegliamo il sistema di assi come in figura sopra e scriviamo le componenti delle forze nelle direzioni x e y:
F1x = F1
F1y = 0
F2x = – F2 cos 30°
F2y = – F2 sen 30°
Le componenti della risultante R delle forze sono:
Rx = F1x + F2x
Ry = F1y + F2y + P + Fv
Se il barattolo è fermo le componenti Rx e Ry devono essere entrambe NULLE, quindi la condizione di equilibrio è:
Rx = 0 → F1x = – F2x
Ry = 0 → Fv = – (P + F1y + F2y)
Tenendo conto delle espressioni delle componenti delle forze, la condizione in questo cosa specifico si può scrivere:
F1 = – F2x
Fv = – (P + F2y)
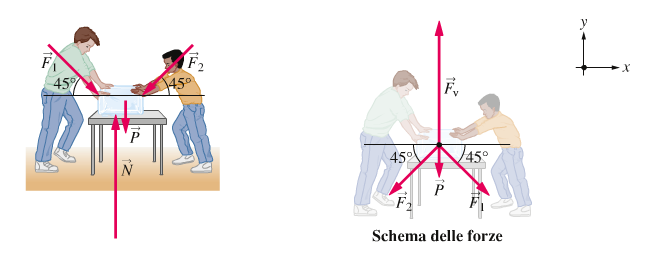 STRATEGIA Per calcolare la reazione vincolare Fv imponiamo la condizione di equilibrio lungo l'asse y:
Rx = 0 → Fv + (P + F1y + F2y) = 0
SOLUZIONE Scriviamo le componenti y delle forze F1 e F2:
F1y = – F1 * sen 45° = – (12 N) * 0,7 = – -8,5 N
F2y = – F2 * sen 45° = – (12 N) * 0,7 = – -8,5 N
Calcoliamo il peso del blocco:
P = – m * g = – (6 Kg)*(9,81 N/Kg) = – 59 N
Sommiamo le componenti y di tutte le forze:
Ry = F1y + F2y + P + Fv = – 8,5 N – 8,5 N – 59 N + Fv = – 76 N + Fv
Poniamo questa somma uguale a zero:
– 76 N + Fv = 0
Infine ricaviamo la reazione vincolare:
Fv = 76 N
OSSERVAZIONI La condizione di equilibrio lungo l'asse x, Rx = 0 → F1x + F2x = 0 è ovviamente soddisfatta, come possiamo facilmente verificare. Infatti:
F1x = F1 * cos 45°
F2x = – F2 * cos 45°
è poichè F1 = F2 otteniamo:
F1x + F2x = F1 * cos 45° – F1 * cos 45° = 0
STRATEGIA Per calcolare la reazione vincolare Fv imponiamo la condizione di equilibrio lungo l'asse y:
Rx = 0 → Fv + (P + F1y + F2y) = 0
SOLUZIONE Scriviamo le componenti y delle forze F1 e F2:
F1y = – F1 * sen 45° = – (12 N) * 0,7 = – -8,5 N
F2y = – F2 * sen 45° = – (12 N) * 0,7 = – -8,5 N
Calcoliamo il peso del blocco:
P = – m * g = – (6 Kg)*(9,81 N/Kg) = – 59 N
Sommiamo le componenti y di tutte le forze:
Ry = F1y + F2y + P + Fv = – 8,5 N – 8,5 N – 59 N + Fv = – 76 N + Fv
Poniamo questa somma uguale a zero:
– 76 N + Fv = 0
Infine ricaviamo la reazione vincolare:
Fv = 76 N
OSSERVAZIONI La condizione di equilibrio lungo l'asse x, Rx = 0 → F1x + F2x = 0 è ovviamente soddisfatta, come possiamo facilmente verificare. Infatti:
F1x = F1 * cos 45°
F2x = – F2 * cos 45°
è poichè F1 = F2 otteniamo:
F1x + F2x = F1 * cos 45° – F1 * cos 45° = 0
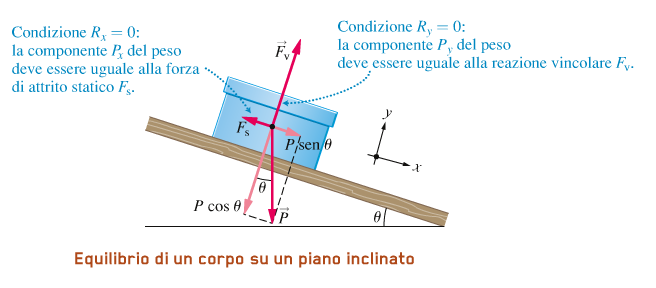 Quando si deve fissare un sistema di coordinate per un piano inclinato, è generalmente preferibile scegliere gli assi x e y rispettivamente parallelo e
perpendicolare alla superfcie stessa. Con questa scelta del sistema di coordinate non c'è alcun moto in direzioney e la reazione vincolare Fv punta nel verso positivo delle y.
Se la superficie del piano è inclinata di un angolo θ, le componenti del peso P lungo gli assi sono:
Px = P * sen θ
Py = – P * cos θ
La condizione Rx = 0 equivale a:
Rx = 0
Ry = 0
Le condizioni Rx = 0 richiede che la componente x del peso Px = P * sen θ, sia compensata da una forza opposta, che nel caso mostrato in figura è la forza di attrito statico Fs:
Rx = 0 → P * sen θ – Fs = 0 → Fs = P * sen θ
Le condizioni Ry = 0 richiede che la componente y del peso Py = P * cos θ, sia compensata dalla reazione vincolare Fv, perpendicolare al piano inclinato:
Ry = 0 → Fv – P * cos θ = 0 cioè Fv = P * cos θ
Quando si deve fissare un sistema di coordinate per un piano inclinato, è generalmente preferibile scegliere gli assi x e y rispettivamente parallelo e
perpendicolare alla superfcie stessa. Con questa scelta del sistema di coordinate non c'è alcun moto in direzioney e la reazione vincolare Fv punta nel verso positivo delle y.
Se la superficie del piano è inclinata di un angolo θ, le componenti del peso P lungo gli assi sono:
Px = P * sen θ
Py = – P * cos θ
La condizione Rx = 0 equivale a:
Rx = 0
Ry = 0
Le condizioni Rx = 0 richiede che la componente x del peso Px = P * sen θ, sia compensata da una forza opposta, che nel caso mostrato in figura è la forza di attrito statico Fs:
Rx = 0 → P * sen θ – Fs = 0 → Fs = P * sen θ
Le condizioni Ry = 0 richiede che la componente y del peso Py = P * cos θ, sia compensata dalla reazione vincolare Fv, perpendicolare al piano inclinato:
Ry = 0 → Fv – P * cos θ = 0 cioè Fv = P * cos θ
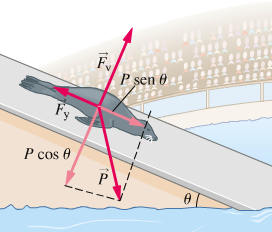 SOLUZIONE Il peso del leone marino è:
P = (450 Kg) * (9,81 N/Kg) = 4400 N
Se il leone marino è fermo, la reazione vincolare Fv è uguale alla componente Py:
Fv = P * cos θ = 4400 N * cos 12° = 4400 * 0,98 = 4300 N
Se il leone marino è fermo, la forza di attrito statico su di esso è uguale alla componente Px:
Fs = P * sen θ = 4400 N * sen 12° = 4400 * 0,21 = 914 N
SOLUZIONE Il peso del leone marino è:
P = (450 Kg) * (9,81 N/Kg) = 4400 N
Se il leone marino è fermo, la reazione vincolare Fv è uguale alla componente Py:
Fv = P * cos θ = 4400 N * cos 12° = 4400 * 0,98 = 4300 N
Se il leone marino è fermo, la forza di attrito statico su di esso è uguale alla componente Px:
Fs = P * sen θ = 4400 N * sen 12° = 4400 * 0,21 = 914 N
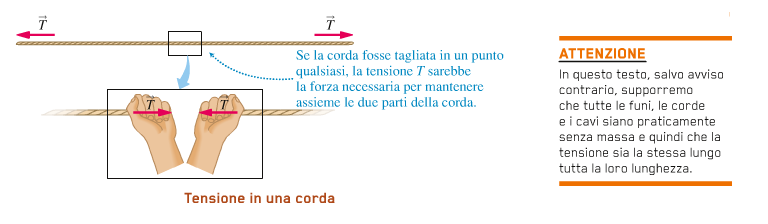 Notiamo che, in un qualsiasi punto della corsa, la tensione è la stessa a destra e a sinistra e, se la corda ha una massa trascurabile, la tensione è la stessa in ogni punto.
Consideriamo ora una corda attaccata con un estremo al soffitto e con l'altro a una scatola di peso P. La corda agisce da vincolo, mantenendo la scatola ferma:
Notiamo che, in un qualsiasi punto della corsa, la tensione è la stessa a destra e a sinistra e, se la corda ha una massa trascurabile, la tensione è la stessa in ogni punto.
Consideriamo ora una corda attaccata con un estremo al soffitto e con l'altro a una scatola di peso P. La corda agisce da vincolo, mantenendo la scatola ferma:
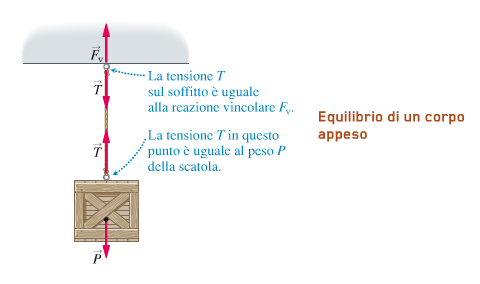 Per la condizione generale di equilibrio, la tensione nel punto in cui è attaccata la scatola deve essere uguale al peso della scatola stessa:
T = P
La tensione sul soffitto è diretta verso il basso ed è bilanciata dalla reazione vincolare Fv del soffitto:
T = Fv
Possiamo verificare facilmente che la forza vincolare ha la stessa intensità del poso del corpo appendendo il corpo a un dinamometro.
Spesso per modificare la direzione della forza esercitata da una corda, vengono utilizzate delle carrugole. Nel caso ideale, una carrucola non ha massa, ne attriti negli ingranaggi.
Una carrucola ideale cambia semplicemente la direzione della tensione in una corda, senza modificare la sua intensità:
Per la condizione generale di equilibrio, la tensione nel punto in cui è attaccata la scatola deve essere uguale al peso della scatola stessa:
T = P
La tensione sul soffitto è diretta verso il basso ed è bilanciata dalla reazione vincolare Fv del soffitto:
T = Fv
Possiamo verificare facilmente che la forza vincolare ha la stessa intensità del poso del corpo appendendo il corpo a un dinamometro.
Spesso per modificare la direzione della forza esercitata da una corda, vengono utilizzate delle carrugole. Nel caso ideale, una carrucola non ha massa, ne attriti negli ingranaggi.
Una carrucola ideale cambia semplicemente la direzione della tensione in una corda, senza modificare la sua intensità:
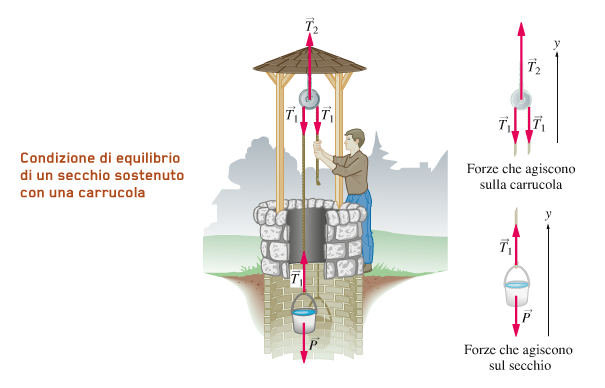
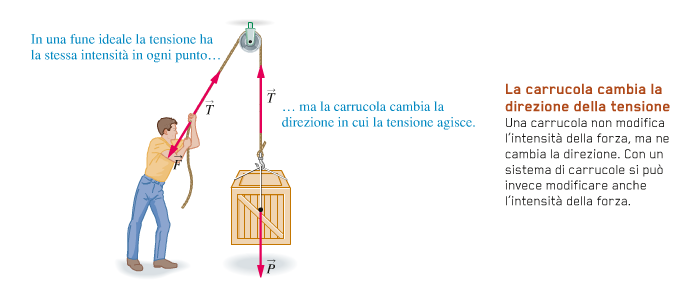 Vediamo un altro caso: una persona regge un secchio d'acqua, utilizzando una funa che scorre su una carrucola. Se il secchio è fermo, qual è la tensione T1 nella fune
attaccata al secchio e qual è la tensione T2 nel cavo che sostiene la carrucola?
Poichè il secchio e la carrucola sono in equilibrio, la forza risultante su ciascuno di essi deve essere zero.
Nel figura vediamo che sul secchio agiscono due forze: il peso P diretto verso il basso e la tensione T1, diretta verso l'alto.
Vediamo un altro caso: una persona regge un secchio d'acqua, utilizzando una funa che scorre su una carrucola. Se il secchio è fermo, qual è la tensione T1 nella fune
attaccata al secchio e qual è la tensione T2 nel cavo che sostiene la carrucola?
Poichè il secchio e la carrucola sono in equilibrio, la forza risultante su ciascuno di essi deve essere zero.
Nel figura vediamo che sul secchio agiscono due forze: il peso P diretto verso il basso e la tensione T1, diretta verso l'alto.
 La condizione di equilibrio è:
T1 – P = 0 → T1 = P
Quindi la tensione e il peso devono avere la stessa intensità.
Notiamo che questa è anche l'intensità della forza che la persona deve esercitare sulla fune verso il basso, come ci aspettavamo.
Nella figura vediamo che sulla carrucola agiscono TRE forze: la tensione T2 nel cavo, diretta verso l'alto, le tensione T1 nella parte di fune attaccata al secchio,
verso il basso, e la tensione T1 nella parte di fune tirata dalla persona, verso il basso.
Non abbbiamo incliso il peso della carrucola, perchè la consideriamo ideale, cioè priva di massa.
La risultante delle forze deve essere NULLA:
T2 – T1 – T1 = 0 → T2 = 2 * T1 = 2 * P
La tensione T2 nel cavo che sostiene la carrucola è quindi il doppio del peso del secchio.
La condizione di equilibrio è:
T1 – P = 0 → T1 = P
Quindi la tensione e il peso devono avere la stessa intensità.
Notiamo che questa è anche l'intensità della forza che la persona deve esercitare sulla fune verso il basso, come ci aspettavamo.
Nella figura vediamo che sulla carrucola agiscono TRE forze: la tensione T2 nel cavo, diretta verso l'alto, le tensione T1 nella parte di fune attaccata al secchio,
verso il basso, e la tensione T1 nella parte di fune tirata dalla persona, verso il basso.
Non abbbiamo incliso il peso della carrucola, perchè la consideriamo ideale, cioè priva di massa.
La risultante delle forze deve essere NULLA:
T2 – T1 – T1 = 0 → T2 = 2 * T1 = 2 * P
La tensione T2 nel cavo che sostiene la carrucola è quindi il doppio del peso del secchio.
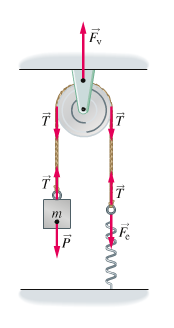 La tensione T nella corda è uguale al peso P del blocco, quindi:
T = P = 2,5 Kg * 9,81 N/Kg = 25 N
Anche la forza elastica della molla è uguale alla tensione nella corda, cioè Fe = 25 N, e quindi l'allungamento della molla è:
x = Fe / k = 25 N / 280 N/m = 0,089 m = 8,9 cm
In condizioni di equilibrio Fv – P – Fe = 0 quindi la reazione vincolare del soffitto è:
Fv = P + Fe = 2P = 50 N
La tensione T nella corda è uguale al peso P del blocco, quindi:
T = P = 2,5 Kg * 9,81 N/Kg = 25 N
Anche la forza elastica della molla è uguale alla tensione nella corda, cioè Fe = 25 N, e quindi l'allungamento della molla è:
x = Fe / k = 25 N / 280 N/m = 0,089 m = 8,9 cm
In condizioni di equilibrio Fv – P – Fe = 0 quindi la reazione vincolare del soffitto è:
Fv = P + Fe = 2P = 50 N
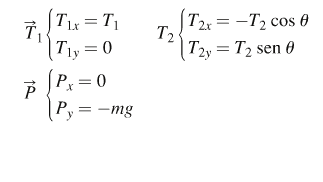
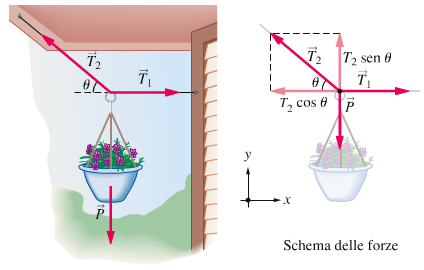 STRATEGIA Il vaso è fermo, quindi la forza risultante R che agisce su di esso è uguale a zero.
Si ha pertanto Rx = 0 ed Ry = 0 .
Quest due condizioni permettono di determinare l'intensità delle due tensioni T1 e T2.
SOLUZIONE Consideriamo l'asse x e impogniamo la condizione Rx = 0.
Questa condizione fornisce una relazione tra T1 e T2:
Rx = 0 → T1x + T2x + Px = T1 + (-T2 * cos θ) + 0 = 0
T1 = T2 * cos θ
Consideriamo l'asse y e imponiamo la condizione Ry = 0; questa volta la condizione permette di determinare T2 in funzione del peso mg:
Ry = 0 → T1y + T2y + Py = T2 + sen θ) + (-mg) = 0
T2 sen θ = mg
Utilizziamo la relazione precedente per determinare T2:
T2 = mg / sen θ = (6,2 Kg * 9,81 N/Kg) / sen 40° = 61 / 0.64 = 94,6 N
Utilizziamo la relazione tra le due tensioni per determinare T1:
T1 = T2 * cos θ = 94,6 N * cos 40° = 94,6 * 0.77 = 72,5 N
OSSERVAZIONI Anche se i cavi che tengono sospeso il vaso sono due, entrambi hanno una tensione maggiore del peso del vaso, mg=60,8N.
Quando un oggetto è appeso a un cavo, è possibile che la tensione nel cavo sia molto più grande del peso dell'oggetto.
Ciò deve essere tenuto in considerazione da architetti e ingegneri quando progettano un edificio.
STRATEGIA Il vaso è fermo, quindi la forza risultante R che agisce su di esso è uguale a zero.
Si ha pertanto Rx = 0 ed Ry = 0 .
Quest due condizioni permettono di determinare l'intensità delle due tensioni T1 e T2.
SOLUZIONE Consideriamo l'asse x e impogniamo la condizione Rx = 0.
Questa condizione fornisce una relazione tra T1 e T2:
Rx = 0 → T1x + T2x + Px = T1 + (-T2 * cos θ) + 0 = 0
T1 = T2 * cos θ
Consideriamo l'asse y e imponiamo la condizione Ry = 0; questa volta la condizione permette di determinare T2 in funzione del peso mg:
Ry = 0 → T1y + T2y + Py = T2 + sen θ) + (-mg) = 0
T2 sen θ = mg
Utilizziamo la relazione precedente per determinare T2:
T2 = mg / sen θ = (6,2 Kg * 9,81 N/Kg) / sen 40° = 61 / 0.64 = 94,6 N
Utilizziamo la relazione tra le due tensioni per determinare T1:
T1 = T2 * cos θ = 94,6 N * cos 40° = 94,6 * 0.77 = 72,5 N
OSSERVAZIONI Anche se i cavi che tengono sospeso il vaso sono due, entrambi hanno una tensione maggiore del peso del vaso, mg=60,8N.
Quando un oggetto è appeso a un cavo, è possibile che la tensione nel cavo sia molto più grande del peso dell'oggetto.
Ciò deve essere tenuto in considerazione da architetti e ingegneri quando progettano un edificio.